Расстояния тонких линз

Лабораторная работа №13

ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО

РАССТОЯНИЯ ТОНКИХ ЛИНЗ

Цель работы: определить фокусное расстояние собирающей линзы

Задачи работы: изучить некоторые методы определения фокусного расстояния тонких линз, научиться строить изображение предмета в тонкой линзе, изучить устройство оптического прибора – глаза.

Приборы и принадлежности: оптическая скамья с набором рейтеров, осветитель с источником питания, экран, собирающая линза, рулетка.

Основные законы геометрической оптики

Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет.

На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а часть пройдет через границу и продолжит распространяться во второй среде.

Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.

Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред:

Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом в 1621 г.

Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.

Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:

n = n ₂ / n ₁.

Законы отражения и преломления находят объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ₁ к скорости их распространения во второй среде υ₂:

Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света υ в среде:

Среду с меньшим абсолютным показателем преломления называют оптически менее плотной.

При переходе света из оптически более плотной среды в оптически менее плотную n ₂ < n ₁ (например, из стекла в воздух) можно наблюдать явление полного отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол α_пр, который называется предельным углом полного внутреннего отражения (см. рис. 3.1.2).

Для угла падения ; значение .

Если второй средой является воздух (n ₂ ≈ 1), то формулу удобно переписать в виде

sin α_пр = 1 / n,

где n = n ₁ > 1 – абсолютный показатель преломления первой среды.

Для границы раздела стекло–воздух (n = 1,5) критический угол равен α_пр = 42°, для границы вода–воздух (n = 1,33) α_пр = 48,7°.

Рис. 2. Полное внутреннее отражение света на границе вода–воздух; S – точечный источник света

Явление полного внутреннего отражения находит применение во многих оптических устройствах. Наиболее интересным и практически важным применением является создание волоконных световодов, которые представляют собой тонкие (от нескольких микрометров до миллиметров) произвольно изогнутые нити из оптически прозрачного материала (стекло, кварц). Свет, попадающий на торец световода, может распространяться по нему на большие расстояния за счет полного внутреннего отражения от боковых поверхностей. Научно-техническое направление, занимающееся разработкой и применением оптических световодов, называется волоконной оптикой.

Линзы

Линза – это один из основных элементов оптических систем, предназначенных для получения оптических изображений. Она представляет собой оптически прозрачное тело (например, из стекла), ограниченное с двух сторон преломляющими (чаще всего сферическими) поверхностями. Если расстояние О ₁ О ₂ (рис. 4) между этими поверхностями значительно меньше радиусов кривизны, то линза называется тонкой. Ее вершины О ₁ и О ₂ в этом случае можно считать совпадающими в точке О, называемой оптическим центром линзы. Причем ось, проходящая через оптический центр линзы и центры кривизны ее преломляющих поверхностей, называется главной оптической осью линзы (прямая РР ¢, рис. 4).

Если направить луч света параллельно главной оптической оси (вблизи нее), то преломившись, он пройдет через точки F ₁ или F ₂ (в зависимости от того, слева или справа от линзы падает на нее луч), лежащие на главной оптической оси линзы. Эти точки называют главными фокусами линзы, а сама линза, преломляющая лучи таким образом, называется собирающей (рис. 4, а). Если же после преломления светового луча линзой через точки F ₁ или F ₂ (главные фокусы) можно провести лишь прямую, представляющую продолжение преломленного луча в направлении, обратном направлению его распространения, то такая линза называется рассеивающей (рис. 4, б).

Расстояние между оптическим центром линзы и ее главными фокусами (расстояния f ₁ или f ₂) называют главными фокусными расстояниями линзы. Они равны между собой, т.е. f ₁ = f ₂ = f, если слева и справа от линзы находится одна и та же среда (например воздух).

Оптическая сила — величина, характеризующая преломляющую способность линз и систем линз. Измеряется в диоптриях (в СИ): 1 дптр=1 м^-1. Обратно пропорциональна фокусному расстоянию системы:

где - фокусное расстояние линзы, а - показатель преломления окружающей среды. Оптическая сила положительна у собирающих систем и отрицательна в случае рассеивающих.

Построение изображения в тонкой линзе

1. Дан условный чертёж, на котором изображены: предмет, тонкая собирающая линза, её оптическая ось, отмечены её фокусы. Необходимо построить изображение предмета.

1.1. Провести луч, идущий из предмета в сторону линзы параллельно главной оптической оси. После линзы этот луч преломится и пройдёт через фокус.

1.2. Провести второй луч, идущий из предмета в сторону линзы через её оптический центр. После линзы этот луч не преломится.

1.3. На пересечении двух построенных лучей будет изображение предмета (Точка А'). Опустить перпендикуляр из точки А' на оптическую ось. Полученная точка – это точка В'. Изображение построено.

2. Если лучи не сходятся справа, то следует провести их продолжения слева.

3. Если дана рассеивающая линза вместо собирающей, то первый луч после линзы начнёт удаляться от оптической оси так, что его продолжение пройдёт через левый фокус. В этом случае также следует провести продолжение этого луча слева от линзы.

Глаз как оптический инструмент

Глаз человека представляет собой сложную оптическую систему, которая по своему действию аналогична оптической системе фотоаппарата. Схематическое устройство глаза представлено на рис. Глаз имеет почти шарообразную форму и диаметр около 2,5 см. Снаружи он покрыт защитной оболочкой 1 белого цвета – склерой. Передняя прозрачная часть 2 склеры называется роговицей. На некотором расстоянии от нее расположена радужная оболочка 3, окрашенная пигментом. Отверстие в радужной оболочке представляет собой зрачок. В зависимости от интенсивности падающего света зрачок рефлекторно изменяет свой диаметр приблизительно от 2 до 8 мм, т.е. действует подобно диафрагме фотоаппарата. Между роговицей и радужной оболочкой находится прозрачная жидкость. За зрачком находится хрусталик 4 – эластичное линзоподобное тело. Особая мышца 5 может изменять в некоторых пределах форму хрусталика, изменяя тем самым его оптическую силу. Остальная часть глаза заполнена стекловидным телом. Задняя часть глаза – глазное дно, оно покрыто сетчатой оболочкой 6, представляющей собой сложное разветвление зрительного нерва 7 с нервными окончаниями – палочками и колбочками, которые являются светочувствительными элементами.

Лучи света от предмета, преломляясь на границе воздух–роговица, проходят далее через хрусталик (линзу с изменяющейся оптической силой) и создают изображение на сетчатке.

Роговица, прозрачная жидкость, хрусталик и стекловидное тело образуют оптическую систему, оптический центр которой расположен на расстоянии около 5 мм от роговицы. При расслабленной глазной мышце оптическая сила глаза приблизительно равна 59 дптр, при максимальном напряжении мышцы – 70 дптр.

Основная особенность глаза как оптического инструмента состоит в способности рефлекторно изменять оптическую силу глазной оптики в зависимости от положения предмета. Такое приспособление глаза к изменению положения наблюдаемого предмета называется аккомодацией.

Область аккомодации глаза можно определить положением двух точек:

• дальняя точка аккомодации определяется положением предмета, изображение которого получается на сетчатке при расслабленной глазной мышце. У нормального глаза дальняя точка аккомодации находится в бесконечности.
• ближняя точка аккомодации – расстояние от рассматриваемого предмета до глаза при максимальном напряжении глазной мышцы. Ближняя точка нормального глаза располагается на расстоянии 10–20 см от глаза. С возрастом это расстояние увеличивается.

Кроме этих двух точек, определяющих границы области аккомодации, у глаза существует расстояние наилучшего зрения, т. е. расстояние от предмета до глаза, при котором удобнее всего (без чрезмерного напряжения) рассматривать детали предмета (например, читать мелкий текст). Это расстояние у нормального глаза условно полагают равным 25 см.

При нарушении зрения изображения удаленных предметов в случае ненапряженного глаза могут оказаться либо перед сетчаткой (близорукость), либо за сетчаткой (дальнозоркость)

Расстояние наилучшего зрения у близорукого глаза меньше, а у дальнозоркого больше, чем у нормального глаза. Для исправления дефекта зрения служат очки. Для дальнозоркого глаза необходимы очки с положительной оптической силой (собирающие линзы), для близорукого – с отрицательной оптической силой (рассеивающие линзы).

Для наблюдения удаленных предметов оптическая сила линз должна быть такой, чтобы параллельные пучки фокусировались на сетчатке глаза. Глаз должен видеть через очки мнимое прямое изображение удаленного предмета, находящееся в дальней точке аккомодации данного глаза. Если, например, дальняя точка аккомодации близорукого глаза находится на расстоянии 80 см, то применяя формулу тонкой линзы получим: d = ∞, f = –0,8 м, следовательно, .

Следует отметить, что у дальнозоркого глаза дальняя точка аккомодации мнимая, т. е. ненапряженный глаз фокусирует на сетчатке сходящийся пучок лучей. Потому при рассмотрении удаленных предметов очки для дальнозоркого глаза должны превращать параллельный пучок лучей в сходящийся, т. е. обладать положительной оптической силой.

Очки для «ближнего зрения» (например, для чтения) должны создавать мнимое изображение предмета, находящегося на расстоянии d ₀ = 25 см (т. е. на расстоянии наилучшего зрения нормального глаза), на расстоянии наилучшего зрения данного глаза. Пусть, например, близорукий глаз имеет расстояние наилучшего зрения 16 см. По формуле тонкой линзы получим: d = d ₀ = 0,25 м, f = –0,16 м, следовательно, Вследствие сужения области аккомодации у многих людей очки для ближнего зрения должны обладать большей (по модулю) оптической силой по сравнению с очками для рассматривания удаленных предметов.

Экспериментальная установка и методы измерения

фокусных расстояний

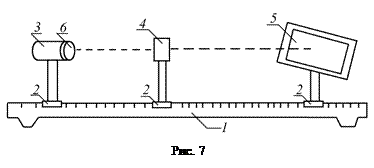Главное фокусное расстояние тонких линз можно измерить различными способами. Для этой цели может использоваться установка, представленная на рис. 7. Установка состоит из оптической скамьи 1, на которой с помощью рейтеров 2 располагаются осветитель 3, исследуемая линза или система линз 4 и экран 5. В качестве предмета, изображение которого проектируется линзой на экран, используется спираль лампы, расположенной внутри осветителя.

Располагая на оптической скамье собирающую линзу, получим на экране действительное изображение предмета (спирали лампы). При этом ход лучей в линзе имеет вид, представленный на рис. 8.

Запишем формулы тонкой линзы (1)–(3)

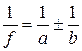, (1)

где f – главное фокусное расстояние линзы; а – расстояние от предмета до оптического центра линзы; b – расстояние от изображения до оптического центра линзы.

Из (1) следует, что

. (2)

Очевидно, что формула (2) может быть использована как рабочая для определения главного фокусного расстояния собирающей тонкой линзы, для чего достаточно измерить лишь расстояния а и b. Следует, однако иметь в виду, что измеряя расстояния от предмета и изображения до оптического центра линзы, мы допускаем ошибку порядка толщины линзы. Поэтому измерение главного фокусного расстояния тонкой линзы имеет смысл только с точностью до ее толщины.

В практике научного эксперимента часто используется иной метод определения главного фокусного расстояния собирающих тонких линз, разработанный Бесселем и получивший название метода Бесселя. Рассмотрим этот метод.

Пусть расстояние между предметом и экраном превышает 4 f. Нетрудно убедиться, что в этом случае всегда найдутся два таких положения линзы (рис. 9), при которых на экране получаются отчетливые изображения предмета (в одном случае увеличенное, в другом – уменьшенное). Поскольку в обоих случаях изображения предмета на экране получаются с помощью одной и той же линзы, то на основе формулы (1) можно записать

(3)

или

. (4)

Но, как следует из рис. 4

а ₁ + b ₁ = а ₂ + b ₂ = L; (5)

а ₁ – b ₁ = а ₂ – b ₂ = l. (6)

Тогда с учетом (5) выражение (4) примет вид

а ₁ b ₁ = а ₂ b ₂, (7)

или, выразив а ₂ и b ₂ через l из (6), получим

а ₁ b ₁ = (l + а ₁)(b ₁ – l), (8)

откуда следует, что

b ₁ - а ₁ = l. (9)

Таким образом, учитывая (5) и (9), составляем систему уравнений:

(10)

решив которую, будем иметь:

. (11)

Подставляя эти значения а ₁ и b ₁ в формулу (3), находим

. (12)

Формула (12) является рабочей для определения главного фокусного расстояния собирающей линзы методом Бесселя.

Дата добавления: 2015-08-26