А) б) в)

Рис. У.3. Кинематические пары для преобразования вращательного движения в поступательное:

а – винтовая; б – зубчато-реечная; в – червячно-реечная

Вращательное движение преобразуется в прямолинейное также с помощью других передач и ряда механизмов (кривошипно-шатунных, кривошипно-кулисных, кулачковых и др.).

2.2.1.3 Совокупность передач привода определяет движение рабочих органов, т.е. кинематику их, и её называют кинематической цепью. В кинематические цепи могут входить как отдельные передачи, так и группы передач (групповые передачи).

Произвольный пример кинематической цепи, состоящей из клиноременной, четырёх зубчатых и цепной передач, приведён на рис. У.4.

Полное передаточное отношение кинематической цепи равно произведению передаточных отношений всех кинематических пар, составляющих цепь.

Полное передаточное отношение I кинематической цепи, показанной в качестве примера на рис. У.4, будет равно:

,

здесь Z₈ и Z₉ – числа зубьев звёздочек цепной передачи.

Направление передачи движения записывается в виде т.н. расчётного перемещения или расчётных перемещенийконечных звеньев.

Так, если n_о и n – частоты вращения ведущего и ведомого валов или начального и конечного звеньев кинематической цепи, то расчётное перемещение представляют в виде: n_о®n. А если n_о и S – частота вращения ведущего вала кинематической цепи и скорость перемещения ведомого звена – гайки винтовой передачи шага t, то расчётное перемещение будет: n_о®S(подробнее см. п. 3.2).

Очевидно, в первом случае – n = n_о×I, а во втором – S = n_о×I×t.

То или иное из этих или им подобных выражений с подробно расписанной правой частью (т.е. вместо I – произведение передаточных отношений всех кинематических пар, составляющих цепь, в виде обозначений шестерён, шкивов или конкретных чисел зубьев шестерён, диаметров шкивов, в последнем случае – и конкретных значений частот вращения, шагов резьб и т.д.) называют уравнением кинематического баланса.

Рис. У.4. Пример кинематической цепи

Для приведённой выше кинематической цепи уравнение кинематического баланса в общем виде и в предположительно возможном числовом будет:

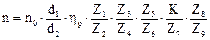и

Уравнение кинематического баланса позволяет определить перемещение конечного звена в зависимости от перемещения начального звена и полного передаточного отношения кинематической цепи, связывающей эти звенья, а при наличии передач, преобразующие вращательное движение в прямолинейное – и их параметров.

2.2.1.4 Условное изображение кинематических цепей всех механизмов станка называют кинематической схемой данного станка.

Кинематические схемы могут быть пространственными и плоскими; первые более наглядны, вторые – проще в исполнении и потому встречаются чаще. Повышение наглядности плоских схем может быть достигнуто при продуманном их исполнении.

Кинематическую схему следует вписывать в габариты или контуры важнейшей проекции станка, сохраняя, по возможности, относительное расположение его отдельных механизмов.

Главная цель кинематической схемы – создание ясного представления о кинематике станка. Этой цели подчинено всё остальное, поэтому при вычерчивании плоской схемы допускаются такие условности, которые, способствуя уяснению кинематики станка, не вполне согласуются с реальной конструкцией его. К примеру, вал, изображаемый обычно прямой линией, может быть показан изогнутым. Допускается полуконструктивное изображение отдельных элементов и частей приводов и узлов станка. Такие подходы проявлены при выполнении кинематических схем данного пособия.

Кинематические схемы станков, несмотря на ряд упрощений и условностей при изображении их, дают простое и наглядное представление не только о кинематике станков, но в некоторой степени и об их конструкции. При соблюдении определённых правил и при внимательном отношении к составлению кинематической схемы она может быть понятна почти без всяких дополнительных пояснений, если известен принцип работы станка.

Дата добавления: 2015-08-26