
Читайте также:
|
Физико-математическая количественная интерпретация электромагнитных зондирований, которая, в основном, сводится к решению обратной задачи, хорошо разработана для одномерных (горизонтально слоистых) моделей сред (см. 7.3). В результате получаются параметры: послойные мощности ( ), сопротивления (
), сопротивления ( ), поляризуемости (
), поляризуемости ( ) или обобщенные для толщи (мощности
) или обобщенные для толщи (мощности  , продольные проводимости
, продольные проводимости  , продольные удельные сопротивления
, продольные удельные сопротивления  , поперечные сопротивления
, поперечные сопротивления  , поперечные удельные сопротивления
, поперечные удельные сопротивления  ). Существуют различные методы решения обратных задач: графоаналитические, палеточные и с помощью ЭВМ (машинные) (см. 7.3.1).
). Существуют различные методы решения обратных задач: графоаналитические, палеточные и с помощью ЭВМ (машинные) (см. 7.3.1).
1. Графоаналитические методы. В результате анализа решений прямых задач ЭМЗ получены аналитические способы расчета обобщенных параметров разреза по асимптотическим или экстремальным значениям КС на кривых ЭМЗ, получившие название графоаналитических.
Наибольшее применение находит метод  . Если кривая ЭМЗ получена над разрезом с очень высоким сопротивлением в основании (например, кристаллическим фундаментом), то проведя под углом 45
. Если кривая ЭМЗ получена над разрезом с очень высоким сопротивлением в основании (например, кристаллическим фундаментом), то проведя под углом 45  (для ВЭЗ-ДЗ) или 63
(для ВЭЗ-ДЗ) или 63  (для МТЗ, ЧЗ, ЗС) к правой ветви кривой асимптоту, можно определить суммарную продольную проводимость (
(для МТЗ, ЧЗ, ЗС) к правой ветви кривой асимптоту, можно определить суммарную продольную проводимость (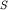 ) толщи над ним. Величина
) толщи над ним. Величина 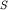 равняется
равняется  (для ВЭЗ, ДЗ),
(для ВЭЗ, ДЗ),  (для МТЗ),
(для МТЗ),  (для ЧЗ в дальней волновой зоне),
(для ЧЗ в дальней волновой зоне),  (для ЗСД),
(для ЗСД), 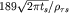 (для ЗСБ), где
(для ЗСБ), где 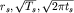 - абсциссы, а
- абсциссы, а  - ординаты любой точки асимптоты.
- ординаты любой точки асимптоты.
На рис. 3.10 по правой асимптоте 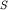 = 330 (1/Ом). Зная
= 330 (1/Ом). Зная 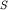 и определив среднее продольное сопротивление этой толщи (
и определив среднее продольное сопротивление этой толщи ( ), например, по параметрическим ЭМЗ у скважин, путем анализа связей перед асимптотой с
), например, по параметрическим ЭМЗ у скважин, путем анализа связей перед асимптотой с  (обычно
(обычно  ) и другими способами, можно рассчитать глубину залегания высокоомного горизонта
) и другими способами, можно рассчитать глубину залегания высокоомного горизонта  . В рассматриваемом нами примере (см. рис. 3.10)
. В рассматриваемом нами примере (см. рис. 3.10)  м.
м.
Существует ряд и других графоаналитических приемов определения различных параметров разреза.
2. Палеточные методы. 1). Палеточные методы интерпретации, применяющиеся в электроразведке долгие годы, основаны на использовании альбомов трехслойных кривых (палеток), различных для разных ЭМЗ и рассчитанные для горизонтально-слоистых моделей сред (см. 9.1.1). Сущность палеточных способов сводится к последовательному совмещению выстроенной на кальке полевой кривой с теоретическими кривыми. Они должны быть построены в одинаковом логарифмическом масштабе. Добившись наилучшего совмещения по индексам совпавшей теоретической кривой и палетки, определяют мощность ( ) и удельное электрическое сопротивление (
) и удельное электрическое сопротивление ( ) первого (верхнего) слоя, относительные значения мощности
) первого (верхнего) слоя, относительные значения мощности  и сопротивления
и сопротивления  второго слоя, а также
второго слоя, а также  интерпретируемой кривой. Отсюда можно найти приближенные значения изучаемого разреза:
интерпретируемой кривой. Отсюда можно найти приближенные значения изучаемого разреза:  .
.
При интерпретации многослойных кривых они с помощью так называемых вспомогательных палеток последовательно (сверху-вниз) разбиваются на трехслойные. Для этого сначала два верхних слоя заменяются одним эквивалентным, т.е. таким фиктивным слоем мощностью  и сопротивлением
и сопротивлением  , чтобы электромагнитное поле на земной поверхности оставалось тем же. Далее три верхних слоя заменяются новым эквивалентным с мощностью
, чтобы электромагнитное поле на земной поверхности оставалось тем же. Далее три верхних слоя заменяются новым эквивалентным с мощностью 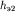 и сопротивлением
и сопротивлением  и так далее. Используя трехслойные теоретические палетки, полученные эквивалентные трехслойные кривые интерпретируют как обычные трехслойные.
и так далее. Используя трехслойные теоретические палетки, полученные эквивалентные трехслойные кривые интерпретируют как обычные трехслойные.
В результате интерпретации кривых ЭМЗ с помощью альбомов палеток получается набор физико-геометрических параметров:  , по которым можно определить приближенные послойные значения мощностей и сопротивлений:
, по которым можно определить приближенные послойные значения мощностей и сопротивлений:

| (3.12) |
Они близки к истинным лишь при  3 - 5, а с уменьшением
3 - 5, а с уменьшением  погрешности в определении послойных параметров разреза резко возрастают. Это объясняется некорректностью решения обратной задачи электроразведки, как и любой задачи математической физики, и существованием принципа эквивалентности, т.е. неоднозначности интерпретации и возможности соответствия одной кривой ЭМЗ множеству геоэлектрических разрезов. Пути его учета рассмотрены ниже (см. 9.1.3).
погрешности в определении послойных параметров разреза резко возрастают. Это объясняется некорректностью решения обратной задачи электроразведки, как и любой задачи математической физики, и существованием принципа эквивалентности, т.е. неоднозначности интерпретации и возможности соответствия одной кривой ЭМЗ множеству геоэлектрических разрезов. Пути его учета рассмотрены ниже (см. 9.1.3).
2). Ускоренная интерпретация кривых ЭМЗ может проводиться с помощью номограмм-палеток, подготовленных В.К.Хмелевским для каждого метода ЭМЗ. Они позволяют заменять при интерпретации громоздкие альбомы палеток (в разных методах ЭМЗ наборы типичных трехслойных кривых меняются от нескольких десятков до сот листов) одной-двумя номограммами-палетками. На рис. 3.11 приведена номограмма-палетка для интерпретации кривых вертикальных (ВЭЗ) и дипольных, азимутальных и экваториальных (ДАЗ и ДЭЗ) зондирований на постоянном токе. Она состоит из вспомогательной (слева) и двухслойной (справа) палеток, объединенных общим началом координат (крест палетки). На вспомогательной палетке приведены шкалы следующих параметров и соответствующие им кривые: а) слева шкала  , оцифровывающая кривые равных значений
, оцифровывающая кривые равных значений  для всех типов трехслойных кривых
для всех типов трехслойных кривых  ; б) сверху приведены шкалы
; б) сверху приведены шкалы  , а внизу -
, а внизу -  для сплошных и пунктирных вертикальных или почти вертикальных кривых
для сплошных и пунктирных вертикальных или почти вертикальных кривых  на номограмме. На двухслойной палетке по оси
на номограмме. На двухслойной палетке по оси  отложены разносы, нормированные мощностью верхнего слоя (
отложены разносы, нормированные мощностью верхнего слоя ( ), а по оси
), а по оси  - значения
- значения  , шкала которых расположена крайней справа. Здесь же прочерчены теоретические (палеточные) двухслойные кривые, сплошные (для ВЭЗ, ДАЗ, ДЭЗ).
, шкала которых расположена крайней справа. Здесь же прочерчены теоретические (палеточные) двухслойные кривые, сплошные (для ВЭЗ, ДАЗ, ДЭЗ).

|
| Рис. 3.11. Номограмма-палетка для интерпретации кривых ВЭЗ, ДЭЗ, ДАЗ |
Последовательность интерпретации с помощью номограммы-палетки рассмотрим на примере пятислойной кривой ВЭЗ-ДЭЗ типа KQH, приведенной на рис. 3.10. Для этого она должна быть вычерчена на кальке с логарифмическим масштабом по осям координат с таким же модулем М, как и номограмма-палетка.
· Полевая многослойная кривая разбивается на двухслойные, и самая левая из них (I - II) накладывается на двухслойную палетку. Соблюдая параллельность осей координат палетки и бланка с полевой кривой, добиваются наилучшего ее совмещения с одной из теоретических. На бланк переносится крест палетки - т. О1, координаты которой на осях ординат и абсцисс равны  и
и  . По правой шкале палетки оценивается
. По правой шкале палетки оценивается  .
.
· С двухслойной палеткой совмещается вторая ветвь полевой кривой (II - III), и на бланк вновь переносится крест палетки О2 с координатами  и
и  . Положение точки О1 на номограмме дает уточненные параметры
. Положение точки О1 на номограмме дает уточненные параметры  , значения которых снимаются с соответствующих шкал (в рассматриваемом примере для первой кривой типа
, значения которых снимаются с соответствующих шкал (в рассматриваемом примере для первой кривой типа  эти параметры определяются по шкалам:
эти параметры определяются по шкалам:  по
по 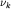 и
и  по левой шкале.
по левой шкале.
· С двухслойной кривой совмещается третья ветвь (III - IV), и на бланк переносится крест палетки О3 ( ), а по положению точки О2 на номограмме определяются
), а по положению точки О2 на номограмме определяются  (в рассматриваемом примере для второй кривой типа
(в рассматриваемом примере для второй кривой типа 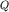 эти параметры определяются по шкалам:
эти параметры определяются по шкалам:  по
по  по
по  .
.
· С двухслойной кривой совмещается четвертая ветвь (IV - V), и на бланк переносится крест палетки О4 (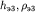 ), а по положению точки О3 на номограмме определяются параметры
), а по положению точки О3 на номограмме определяются параметры  (в рассматриваемом примере для третьей кривой типа
(в рассматриваемом примере для третьей кривой типа  эти параметры определяются по следующим шкалам:
эти параметры определяются по следующим шкалам:  по
по  по
по  .
.
В результате интерпретации с помощью номограммы-палетки получаются те же параметры, что и при палеточной (см. 3.12).
Параметры  определяются по формулам (3.12) и являются приближенными. Для точного их определения необходима дополнительная информация, например, значения
определяются по формулам (3.12) и являются приближенными. Для точного их определения необходима дополнительная информация, например, значения  и т.п. по данным геофизических исследований скважин. В приведенном примере (рис. 3.10) результаты интерпретации следующие (
и т.п. по данным геофизических исследований скважин. В приведенном примере (рис. 3.10) результаты интерпретации следующие (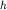 в метрах,
в метрах,  в Омм):
в Омм):  м (с помощью примененного выше метода
м (с помощью примененного выше метода 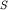
 .
.
3. Машинные методы интерпретации. Интерпретация ЭМЗ с помощью ЭВМ производится с большей точностью, объективностью и скоростью. Существует множество алгоритмов решения обратной задачи ЭМЗ. Наибольшее распространение получили алгоритмы разных вариантов подбора. Принципы их основаны на следующем.
· В ходе предварительной интерпретации (качественной, а лучше с помощью номограмм-палеток) получается априорная информация о геоэлектрическом разрезе: число слоев, примерные значения мощностей и сопротивлений.
· Выбираются те или иные методы и программы решения прямых задач ЭМЗ, которые отличаются точностью и временем счета, этапами ввода дополнительной информации, возможностью использовать различные персональные компьютеры и др. Для получения априорных параметров модели решается прямая задача и теоретическая кривая сравнивается с полевой.
· Добиваются наилучшего совпадения полевой кривой с теоретическими, у которых постепенно меняются параметры. Методом последовательных приближений получают минимум среднеквадратического отклонения или логарифмической невязки кажущихся сопротивлений на всех параметрах глубинности.
· В минимизируемый функционал невязки вводится стабилизатор решения с учетом всех дополнительных геолого-геофизических сведений о районе исследований: минимальные и максимальные мощности, электромагнитные свойства слоев и т.д.
· Выдаются наиболее вероятные значения параметров геоэлектрического разреза (см. 3.12), но более точные, чем рассчитанные по формулам (3.12) и (3.13), благодаря использованию дополнительных данных.
Дата добавления: 2015-08-26; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Качественная интерпретация электромагнитных зондирований. | | | Геолого-геофизическая количественная интерпретация электромагнитных зондирований. |