Электрическое поле точечного источника постоянного тока над двухслойной средой.

Простейшей, но очень важной для практики электроразведки методом сопротивлений, одномерной прямой задачей является задача об электрическом поле и кажущемся сопротивлении на поверхности полупространства, верхнее из которых воздух, а нижнее - двухслойная горизонтально слоистая среда с мощностью верхнего слоя , нижнего , УЭС слоев 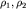и (воздух) (см. рис. 3.3).

Поставленная задача могла бы быть решена с помощью уравнения (3.2), которое при превращается в уравнение Лапласа , где 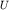- потенциал в любой точке М с напряженностью электрического поля .

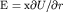Рис.. 3.3. Решение прямой задачи о поле точечного источника постоянного тока над двухслойной средой методом зеркальных отражений

Однако ее можно быстро решить методом зеркальных отражений. 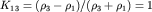Согласно правилам метода зеркальных отражений, урав-нение Лапласа и физические требования, в том числе граничные условия, выполняются, если потенциал в одномерной среде, где расположен точечный источник, принять равным сумме потенциалов этого источника () и всех его многократных отражений от границ раздела () с коэффициентами отражений, равными на границе I , а на границе II (т.к. ).

На рис. 3.3 показано, как эти источники расположены. При этом обозначено

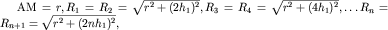
где .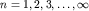

Таким образом, искомое выражение для потенциала получает вид:

(3.9)

Выражение для КС (3.1) можно записать в виде: , где - напряженность электрического поля. Но 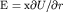, поэтому . Подставив в эту формулу производную из (3.9), получим

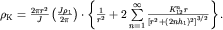
Откуда

(3.10)

Анализируя эту формулу, можно найти асимптотические выражения , равные и . В самом деле, при , при

(т.к. , а равна 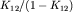как сумма членов геометрической прогрессии).

С помощью формулы (3.10), справедливой для трехэлектродной и симметричной четырехэлектродной градиент-установок, принято строить теоретические двухслойные кривые - графики зависимости ) от . Они называются двухслойными теоретическими кривыми ВЭЗ (вертикальное электрическое зондирование) (см. 8.2), или двухслойной палеткой ВЭЗ (см. рис. 3.4).

Рис. 3.4. Двухслойная палетка ВЭЗ: 1 и 2 - теоретические и полевая кривые

Более громоздкое решение получается в задаче о поле точечного источника над многослойной горизонтально слоистой средой, а еще сложнее решение для такой же среды, но при возбуждении поля дипольными гармоническими или импульсными источниками.

Одномерные прямые задачи электроразведки для многослойных горизонтально слоистых сред для любых первичных полей все-таки сводятся к аналитическим формулам для расчета КС. В результате принято строить кривые КС, аналогичные приведенным на рис. 3.4.

Двухмерные и трехмерные прямые задачи электроразведки сводятся к аналитическим формулам лишь для тел простой формы (шар, пласт, цилиндр) в однородной среде. В более общих случаях получаются лишь приближенные численные решения, получаемые с помощью ЭВМ.

Дата добавления: 2015-08-26