Матрицы

1. Сложение/вычитание идет поэлементно (только для одинаковых по размеру).

2. Умножение числа на матрицу: число умножается на каждый элемент матрицы.

3. Умножение согласованных (не обязательно одинаковых – главное, чтобы число столбцов первой было равно числу строк во второй, при этом у результирующей матрицы будет столько строк, сколько у первой, а столбцов, сколько у второй) матриц:

*

=

С11=ai+bn+cq С12=al+bo+cr С13=am+bp+cs

С21=di+en+fq С22=dl+eo+fr С23=dm+ep+fs

С31=gi+hn+kq С32=gl+ho+kr С33=gm+hp+ks

4. приведение к диагональному виду для решения системы методом Гаусса (здесь d, h, o – столбец свободных членов, тех что после знака «равно»)

a. если a≠0, то первую строчку переписываем как есть (если равно нулю, то меняем первую строку со второй и продолжаем),

b. вместо e и i пишем нули, остальное пересчитываем: вместо f пишем af-be, вместо g пишем ag-ce, вместо h пишем ah-de, вместо m пишем am-bi, вместо n пишем an-ci, вместо o пишем ao-di

c. теперь переписываем первую и вторую строки как есть

d. в третьей строке пишем два нуля, а оставшиеся два элемента пересчитываем из новой матрицы как считали выше (только теперь вместо первого множителя а везде будет число, которое стоит на месте элемента f в новой матрице.

e. из последней матрицы составляем новую систему и из третьего уравнения находим х3

f. затем подставляя х3 во второе уравнение находим х2

g. наконец находим х1

h. система решена

Начиная с пункта e. – алгоритм работает для системы, где 3 уравнения, 3 неизвестных и ранг матрицы коэффициентов при иксах равен рангу расширенной матрицы, т. е. трем (ранг матрицы – это порядок наибольшего НЕ РАВНОГО НУЛЮ определителя, который можно составить из исходной матрицы).

Если ранг матрицы коэффициентов при иксах меньше ранга расширенной, то решений нет.

Если уравнений меньше, чем неизвестных, то решений бесконечное множество, тогда алгоритм начиная с пункта e. немного другой, но думаю на зачете таких не будет.

Если элементы d, h, o в исходной системе равны нулю, то очевидно, что одно из решений, это х1=0, х2=0, х3=0, но может быть и другое решение.

Определители

|A|=aek+dhc+bfg-ceg-fha-dbk

Минор элемента а – это М=ek-fh, минор элемента f – это ah-bg, т. е. определитель, вычисленный после вычеркивания столбца и строки, где находится этот элемент.

Алгебраическое дополнение – это минор элемента, умноженный на (-1) в степени (i+j) (номер строки плюс номер столбца, где находится этот элемент.

Для решения системы матричным способом нужно посчитать определитель матрицы коэффициентов при иксах (матрица А), составить матрицу из алгебраических дополнений, транспонировать эту матрицу (заменить строки столбцами) – получиться матрица А^-1, а затем составить матрицу-столбец иксов по формуле: Х=(1/|A|)*(А^-1*В), где В – матрица-столбец свободных членов (как перемножить матрицы А и В смотри выше.

Длина вектора, заданного одной маленькой буквой:

Длина вектора, заданного двумя буквами А(х1, у1,z1) и В(х2,у2,z2)

Правило Лопиталя: предел отношения функций равен пределу отношения производных этих функций (работает для неопределенностей 0/0 и ∞/∞, для других нужно делать алгебраические преобразования, а затем возвращаться к правилу).

Если нужно найти угловой коэффициент (или тангенс угла наклона) касательной к графику f(x) в точке x₀, это значит нужно найти производную функции, а затем вычислить ее значение, подставив значение x₀.

Таблица производных

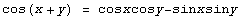
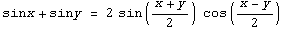
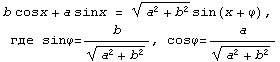
Дата добавления: 2015-08-20