Построим математическую модель транспортной задачи.

1.1. «Составить план перевозок грузов» - значит определить сколько, от куда и куда надо перевезти груза, чтобы достичь поставленной цели - «затраты на эти перевозки были минимальными». Введем управляющие переменные: - количество груза, перевозимого из пункта 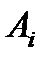в пункт ().

1.2. Стоимость этой перевозки составит . Тогда целевая функция - суммарные затраты, связанные с реализацией всего плана перевозок – запишется выражением:

в общем ви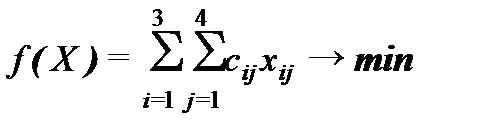де , где

в нашей задаче: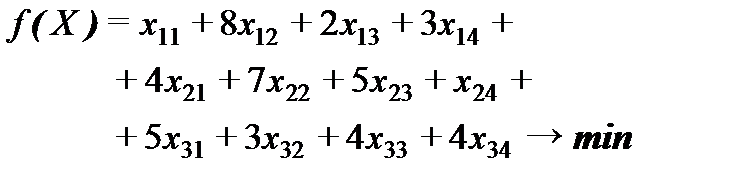

1.3. Для построения системы ограничений проверим, является ли задача сбалансированной.

Суммарная мощность поставщиков Суммарная мощность потребителей

Следовательно, условие сбалансированности не выполнено.

1.4. Запишем систему ограничений:

По потребителю: мощности поставщиков меньше мощности потребителей, следовательно, кто-то из потребителей получит груза меньше, чем его потребность .

Количество груза, которое потребитель действительно получит, запишется выражением: . Так как это меньше, чем его потребность, ограничение будет иметь вид: .

Аналогично строятся ограничения по другим потребителям. Так как в задаче заранее не оговаривается, потребности какого потребителя не будут удовлетворены, знак поставим в ограничениях по всем потребителям. Получим систему ограничений по потребителю:

По поставщику: весь имеющийся на станции отправления груз будет вывезен (т.е. ):

;

Прямые ограничения .

Дата добавления: 2015-08-20