Ответ (В) 40.

Можно решить эту задачу «более красиво». Вот так:

Будем записывать пары чисел следующим образом:

Тогда наши пары чисел такие:

Ведь какое бы А ни было, разность верхнего и нижнего числа будет 50.

Но числа A должны быть (по условию!) двузначными. Это 10, 11, 12 и так далее

Запишем их по-другому:

Номер числа:								…
Число:	9+1	9+2	9+3	9+4	9+5	9+6	9+7	…

Тогда наша пара будет иметь вид:

, где n = 1, 2, 3, 4 …, то есть порядковый номер нашей пары.

Но верхнее число должно быть двузначным. Максимальное двузначное число – 99.

Поэтому максимальный номер находим так:

59 + n = 99 или n = 40

Максимальный порядковый номер – 40. Это и означает, что таких пар – 40.

СПОСОБ ВТОРОЙ – СЧИТАЕМ ГРУППАМИ И ПЕРЕМНОЖАЕМ

Давайте запишем для удобства нашу пару чисел в столбик, как раньше:

Или так:

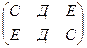- сотни (С) и единицы (Е) переставлены. А вот десятки остались на месте. И это важно!

Пусть мы какую-то пару чисел, удовлетворяющую нашим условиям, например, такую:

Тогда и все числа с «другими» десятками тоже этим условиям удовлетворят!

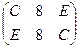
Всего таких чисел – 10. От 0 до 9.

Поэтому, подсчитывая наши «пары», надо подсчитать все пары вида , и умножить результат на 10.

Теперь нетрудно сообразить, что сотни и единицы различаются на 3. 300 – 3 = 297

Наши пары, «представляющие» десятки пар чисел будут такие:

Проверьте, чему равна их разность «в столбик»:

Получится 300 – 3 = 297.

А сколько таких «представителей» может быть?

Е не может быть 0 – числа трехзначные!

Е+3 не может быть 10 и больше – ведь это цифра!

Значит Е принимает значения:

1, 2, 3, 4, 5, 6 (всего 6)

И мы имеем таких «представителей» десяток пар чисел:

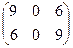
Таким образом, удовлетворяющих условию пар чисел будет 6*10 = 60.

(Г) 60

СПОСОБ ТРЕТИЙ. СЧИТАЕМ НЕ ПО ОДНОМУ!

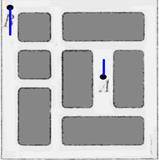
Машина не может приехать «сверху», т.к. для этого нужно совершить левый поворот. Зная, что приехать можно только снизу-вверх …	…давайте уберем дома! Вот что получится. Полный поворот или 4 поворота по 90°. С меньшим числом поворотов проехать нельзя — как бы дома не стояли!
Можно и больше, чем 4: — 8 = 4*2, 12 = 4*3, 16 = 4*4 — кратно 4-м:	Вот ответ, который от вас ожидают.

Всё верно. Но есть и ещё одно решение.

Кто сказал, что машина стоит передом ВВЕРХ? А если ВНИЗ? – туда и придется ехать.

Будет на два поворота больше!

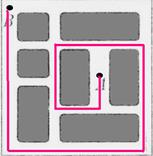
Давайте подумаем, что было бы, если дороги были устроены иначе:

Вот так	Или так

Дата добавления: 2015-08-20