
Читайте также:
|
® 68 ® 85 ® 51 ® 17 ® ТУПИК!

То же самое можно изобразить в виде ориентированного графа!
Число наше длинное, и в самом начале нам надо двигаться по кругу, и на развилке 46 не сворачивать – иначе число станет коротким:

Вот, например, если мы начнём с 69, то последовательность будет такой:
69 ® 92 ® 23 ® 34 ® 46® 69 ® 92® 23 ® 34 ® 46 ® 69 ® 92 ® 23 ® 34 ® 46 ®69 ®
Мы обошли круг три раза, а придется обходить его много-много раз.
Наш маршрут – это и наше число, вернее его начало. Вот оно:
69234692346923469…
Таких начал-кругов ПЯТЬ, по числу кружков с числами. Но вот в самом конце нашего числа нам никто не мешает свернуть на развилке числа 46. И могут получиться дополнительные маршруты (и числа), различающиеся только хвостиками.
Вот, например:
| Обычный (круговой маршрут) | …69 ® 92® 23 ® 34 ® 46 ® 69 ® 92 (стоп) |
| Дополнительный маршрут | …69 ® 92® 23 ® 34 ® 46 ® 68 ® 85 (стоп) |
И таких дополнительных хвостиков несколько. Их можно подсчитать и добавить к пяти последовательностям чисел «по кругу». А их пять, поскольку начать круг мы можем с любого из пяти чисел круга.
Но можно поступить по-другому. ДАВАЙТЕ СЧИТАТЬ С ХВОСТОВ! В обратную сторону! Начнем строить наши числа справа налево.
Тогда наш граф (по которому мы теперь пятимся) будет выглядеть иначе!

Такой маршрут — с конца — абсолютно однозначный. Если мы начнем (а точнее «закончим») с какого-то места, то уже никуда не свернем, нигде не упрёмся в тупик. Начали — и наша последовательность определилась этим началом.
Вот смотрите.
Начнем, например, с 51
51 ® 85 ® 68 ® 46 (попали в круг) ® 34 ® 23 ® 92 ® 69 ® 46 ® 34 (по кругу) ®
А сколько таких начал маршрута «с конца»? Правильно — 9. Ровно столько, сколько кружочков с числами на графе. С любого можно начать!
(Б) 9
ПОВТОРЕНИЕ ПРОЙДЕНОГО!

Можно легко сообразить, что «не отрывая руки» пишутся только Г и Р.
Но те, кто был на прошлом занятии, знают почему!
| Вот, смотрите, букву «Е» не отрывая руки нарисовать нельзя – не две (и не ноль) нечетные вершины. | 
|
| А вот «Р» – можно. Ровно две нечетные вершины! | 
|

Мы увидим самую большую башенку в каждом столбце. Она либо загородит остальные, либо будет торчать поверх тех, которые не смогли ее загородить.
Давайте найдем самую высокую башенку в каждом столбце:
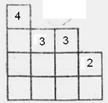 (Д)
(Д)
Дата добавления: 2015-08-20; просмотров: 40 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нечетные | | | ДОМАШНЕЕ ЗАДАНИЕ (ТОПОЛОГИЯ) |