Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Задание к контрольной работе

Читайте также:
  1. II. Прочитайте текст и выполните задание на понимание текста.
  2. IV. Требование к работе
  3. Quot;Актёрское мастерство - Ваш инструмент для бизнеса" «Артистизм - тонкое мастерство в искусстве, виртуозность в работе» Ожегов.
  4. VII. Домашнее задание
  5. VIII. Домашнее задание
  6. XVI Однажды на работе
  7. Агентское задание СОРТИРОВКА ПОСЫЛОК.

по дисциплине «МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ»


Задание к контрольной работе по дисциплине «Методы оптимальных решений»

Номер варианта контрольной работы определяется по порядковому
номеру студента по списку группы

  1. Задача линейного программирования.

Для изготовления двух видов продукции используется три вида сырья. При производстве единицы продукции первого вида затрачивается u1 кг сырья первого вида, u2 кг сырья второго вида и u3 кг сырья третьего вида. При производстве единицы продукции второго вида затрачивается v1 кг сырья первого вида, v2 кг сырья второго вида и v3 кг сырья третьего вида. Запасы сырья первого вида составляют A кг, второго - B, третьего – С кг. Прибыль от реализации единицы продукции первого вида составляет P1 руб, а прибыль от реализации единицы продукции второго вида P2 руб. Построить экономико-математическую модель задачи, максимизирующую прибыль от реализации продукции. Решить задачу геометрически. Построить двойственную задачу и найти ее решение на основе теорем двойственности. Найти решение прям с помощью модуля «Поиск решения» ППП ЭТ MS Excel ой и двойственной задач с помощью модуля «Поиск решения» ППП ЭТ MS Excel. Провести содержательный экономический анализ полученных результатов.

 

№ u1 u2 u3 v1 v2 v3 A B C P1 P2
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       

 

 

2. Транспортная задача.

 

Заданы объемы запасов в пунктах производства, объемы потребностей в пунктах потребления и матрица транспортных издержек по перевозке единицы груза из пункта производства в пункт потребления. Требуется найти оптимальный план перевозок. Построить математическую модель транспортной задачи. Решить задачу, найдя первоначальное распределение поставок одним из методов (методом «наименьших элементов» или методом северо-западного угла) и провести анализ полученного решения.

 

 

1 вариант   2 вариант  
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
3 вариант 4 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
5 вариант 6 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
7 вариант   8 вариант  
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
9 вариант 10 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
11 вариант 12 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
13 вариант   14 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
    15 вариант     16 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
17 вариант 18 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
19 вариант 20 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
21 вариант 22 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
23 вариант 24 вариант
  В1 В2 В3 В4 В5 Запас   В1 В2 В3 В4 В5 Запас
А1             А1            
А2             А2            
А3             А3            
Потр.             Потр.            
25 вариант  
  В1 В2 В3 В4 В5 Запас              
А1                          
А2                          
А3                          
Потр.                          
   

 

  1. Задача нелинейного программирования.

Предпочтения потребителя описываются функцией полезности 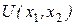, доход равен I, а цены товаров p=(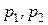). Полагая, что поведение потребителя рационально (то есть он выбирает такие количества каждого блага из товарного набора, которые позволяют ему максимально удовлетворить свои потребности при наличии ограниченного дохода) требуется: определить оптимальный набор товаров, который выберет потребитель при фиксированном доходе и заданном векторе цен, а также достигнутый уровень полезности.

Построить экономико-математическую модель, решить задачу методом множителей Лагранжа и с помощью модуля «Поиск решения» ППП ЭТ MS Excel.

 

Вариант U(x1,x2) P1 P2 I
       
       
       
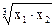
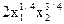
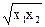
  5x11/3x22/3      
       
       
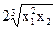
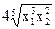
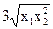
  0.7    
  2х12/5х23/5   2.5  
       
  3(х1-5)1/4х23/4   1.5  
  5х11/4(х2-3)3/4      
  2х13/4(х2-4)1/4      
       
       
       
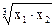
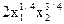
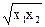
  5x11/3x22/3      
       
       
       
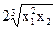
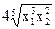
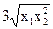
  2х12/5х23/5      
       
  3х11/4(х2-3)3/4      
       
       
       

 

 

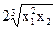
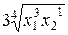
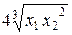
Список рекомендуемой литературы:

1. Экономико-математические методы и прикладные модели. Под редакцией Федосеева В.В. – М.:ЮНИТИ, 1999.-391 с.

2. Исследование операций в экономике. Под редакцией Кремера Н.Ш. – М.:ЮНИТИ, 1999.-407 с.

Дата добавления: 2015-08-20; просмотров: 86 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Комментарии к ключевым проблемам и понятиям курса| Write T for true and F for false sentences. Correct the false statements.
mybiblioteka.su - 2015-2024 год. (0.012 сек.)