Жиілік сипаттамалары

Уақыттық сипаттамалармен қатар жүйенің сапалы анализіне жиіліктік сипаттамасын қолданады. Берілген жағдайда сызықты жүйеге еркін диапазонда өзгеретін a_i амплитуда және w жиілігімен гармоникалық кіріс әсерлер әсер етеді.

x=a_і 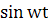(4.6)

Сызықты автоматты басқару жүйелерінде орнықты реакция гармоникалық тәуелділік бойынша өзгеріске түседі.

Жиіліктік сипаттамалар көмегімен АБЖ анализі үшін (2.1) дифференциалды теңдеу жүйесіндегі тік Фурье түрлендіргіші қолданылады:

.

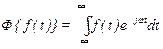Сонымен қатар, жиіліктік түрлендіргіш үшін ресми түрде s – ті jw – ға ауыстырып, Лапластың екі жақты түрлендіргішін қолдануға болады..

Жиіліктік беріліс функциясын W(s) кешенді БФ үшін s – ті jw – ға ауыстыра отырып жәй ғана алуға бролады (2.16), онда:

W(jw)=A(w)e^{j 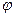(w)}=P(w)+jG(w) (4.7)

Мұндағы A(w), 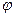(w) – сәйкесінше, жүйенің амплитуда - жиіліктік және фаза – жиіліктік сипаттамалары деп аталады. P(w), G(w) – нақты және жорамал жиілікті сипаттамалар. Функция годографы W(jw) амплитуда-фазалы-жиілікті сипаттамасын (АФЖС) көрсетеді.

Амплитуда - жиілікті сипаттамасы (АФЖ) келесі өрнектен анықталады

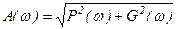(4.8)

Фазалы жиілікті сипаттамасы (ФЖС) төмендегідей анықталады

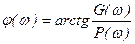(4.9)

Сонымен, 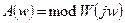модулі (3.8) амплитудалы жиілікті функция болып келеді, ал оның графигі амплитудалы жиілікті сипаттама болады.

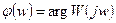(3.9) аргументі фазалы жиілікті функция, ал оның графигі фазалы жиілікті сипаттама болып келеді.

Орнықты жүйелердің гармоникалық әсерлері кезінде өтпелі үрдіс аяқталғаннан кейін шығыс шама басқалармен амплитудамен және фазамен гармоникалық заң бойынша өзгереді. Осы кезде шығыс және кіріс амплитудаларының қатынастарының мәндері 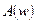модуліне тең, ал фазаның ығысуы жиілікті беріліс функциясының аргументіне 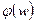тең болады, және сәйкесінше, амплитуда жиіліктік сипаттама амплитуда қатынастарын, ал фазалы жиілікті сипаттама кіріс гармоникалық әсердің жиілігіне тәуелді кіріске қатысты шығыс шамалардың фаза ығысуын көрсетеді.

Жиілікті тәсілдердің артықшылығы, күрделі аналитикалық есептер жүргізбестен эксперименталды жолмен жиілікті сипаттамаларды алу мүмкіндігі болып табылады.

Енді АЖС және ФЖС арасындағы байланысқа көңіл аударайық. Минималды фазалы деп аталынатын кейбір буындар үшін 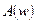және 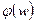функциялары арасында байланыс бар екендігін Боде Г.В. дәлелдеген. Жалпы жағдайда, минималды фазалы деп беріліс функциясының барлық полюстері және нөлдерінде теріс немесе нөлге тең нақты бөліктері бар буындарды айтады. Минималды фазалы буындар орнықты болып келеді.

АЖС логарифмді масштабта децибилде (дБ) көрсету ыңғайлы. Сол кезде, логарифмді амплитудалы жиілікті сипаттаманы (ЛАЖС) келесі өрнектен табылады:

L=(w)=20 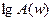(4.10)

Атап өту керек, Бел қуатты он еселі көбейтуге сәйкес келетін логарифмдік бірлікті ұсынады.

Графикалық кескінде ЛАЖС жиіліктерді логарифмдік масштабта абсцисса осі бойына с^-1 немесе Гц өлшемімен орналастырамыз. Жиілік диапазондары октава және декадаға бөлінеді. Октава – бұл бір бірінен 2 есеге өзгеше болатын, жиіліктер арасында қорытындысы болып табылатын жиілік диапазоны. Декада – 10 есеге өзгешелігі бар жиілік үшін арналған диапазон.

Логарифмді амплитудалы жиіліктік сипаттамалардың артықшылығы күрделі есептеу жұмыстарынсыз көптеген жағдайларда АБЖ синтездеу және анализдеу кезінде графикалық кескіндерді құру мүмкіндігі болып табылады.

4.3 – сурет. ЛАЖС және ЛФЖС абсцисса остері

Бұл артықшылық жиілікті беріліс функциясы көбейткіштер туындысы ретінде ұсынылған жағдайларда көрінеді. Сонда, нәтижелі ЛАЖС жеке көбейткіштерге сәйкес келетін ЛАЖС ординаталарының қосындысымен табылуы мүмкін. Көптеген жағдайларда осындай қосындылар қажет болмайды және нәтижелі ЛАЖС 20 дБ/дек еселі көлбеулі түзу сызық қимасының жиынтығы бар асимптоталы ЛАЖС деп аталынатын сипаттама түрінде салынуы мүмкін.

Дата добавления: 2015-08-20