Лабораторна робота 3. Визначення центра ваги плоских фігур

Технічна механіка

МЕТОДИЧНІ ВКАЗІВКИ ДО ЛАБОРАТОРНИХ РОБІТ

Лабораторна робота 3. Визначення центра ваги плоских фігур

Вінниця-2014

Лабораторна робота 3. Визначення центра ваги плоских фігур

Мета роботи: визначити центр ваги складної фігури аналітичним та дослідним шляхом.

Обладнання, інструменти і матеріали: установка для визначення центра ваги способом підвішування; картон; ножиці; креслярське приладдя; лінійка; ПК.

Студент повинен знати:

- способи визначення центра ваги тіл;

- методику експериментального визначення центра ваги плоских тіл способом підвішування.

Студент повинен уміти:

- обчислювати координати центра ваги плоских тіл через статичні моменти площ;

- проводити експериментальне визначення центра ваги плоских тіл.

МЕТОДИЧНІ ВКАЗІВКИ

Матеріальні тіла складаються з елементарних частинок, розміщення яких в просторі визначається їх координатами. Сили тяжіння кожної частинки до Землі можна враховувати системою паралельних сил, рівнодійна цих сил називається силою тяжіння тіла або вагою тіла. Центр ваги тіла – це точка прикладення сили тяжіння. Центр ваги – це геометрична точка, яка може бути розміщена як на тілі так і поза ним (наприклад, диск з отвором, порожній круг і т.д.).

Велике практичне значення має визначення центра ваги тонких, плоских однорідних пластин. Їх товщиною, зазвичай, можна знехтувати і враховувати, що центр тяжіння розміщений в площині. Якщо координатну площину х0у розмістити так, щоб співпадала з площиною фігури, то положення центра ваги визначається двома координатами:

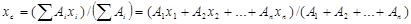, (1)

, (2)

де А_і – площа частини фігури, м²; х_і і у _і – координати центра ваги частин фігури, м.

В таблиці 3.1 приведені площі і координати центрів ваги простих плоских фігур.

Таблиця 3.1. Площі і координати центра ваги плоских фігур

Переріз фігури	А,мм^2	хс , мм	ус, мм
1	2	3	4
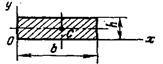
	b·h	b/2	h/2
	b·h/2	b/3	h/3
	R^2·α	(2/3)·R·(sinα/2)	0
При 2α=π π R^2/2	(4/3)·(R/ π)	0

На мал. 3.1 показана однорідна плоска фігура складної форми. Її можна поділити на 4 простих фігури: трикутник, квадрат, напівкруг, прямокутник.

Провівши систему координат х0у, для кожної простої фігури визначаємо координати центра ваги:

C₁(2/3 h; a/2); C₂[(h+a/2); a/2];

C₃[(h + a/2); (a/2+4/3 R/ π)];

С₄[(h+a+d/2); h/2] та їх площі:

А₁ = ah/2; A₂ = a²; A₃ = - R²/2;

A₄ = bH.

Знак мінус у площі показує, що це площа отвору. Координати центра тяжіння всієї фігури обчислюється за формулами (1) і (2).

Рис.3.1. Схема однорідної плоскої фігури.

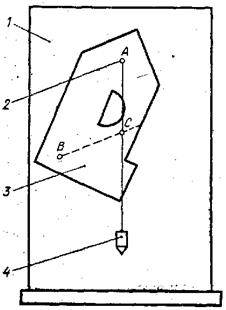Установка для випробування. Установка для дослідного визначення координат центра тяжіння способом підвішування складається з вертикального стояка 1 (Рис.3.2), до якого підвішена голка 2, плоска фігура 3 виготовлена з картону, тонкого металу або іншого матеріалу, в якому можна легко проколоти отвір. Отвір А і В проколюється у довільно розташованих точках (краще на найбільш віддаленій відстані один від одного). Плоска фігура підвішується на голку спочатку в точці А, а потім в точці В. За допомогою відвісу 4, закріпленого на тій же голці, на фігурі прокреслюють олівцем вертикальну лінію, відповідно нитці відвісу. Центр ваги С буде знаходитись в точці перетину вертикальних ліній, нанесених при підвішуванні фігури в точках А і В.

Рис.3.2. Схема установки для випробування.

ПОЯСНЕННЯ ЩОДО ВИКОНАННЯ РОБОТИ

Ознайомитись з будовою установки для визначення центра ваги плоскої фігури.

Накреслити фігуру складної форми, згідно індивідуального завдання (табл. 3.2, рис.3.2), яка складається з 3-4 простих фігур (трикутник, прямокутник, частина круга і т.д.) і вказати її розміри.

Провести вісі координат так, щоб вони захоплювали всю фігуру; розбити складну фігуру на прості частини, визначити площу і координати центру ваги кожної простої фігури відносно вибраної системи координат. Дані записати в таблицю протоколу 1.

Обчислити координати центра ваги всієї фігури аналітично.

Вирізати дану фігуру з тонкого картону або фанери. Просвердлити два отвори, окрайки отворів повинні бути гладенькими, а діаметр отворів не значно більший діаметра голки для підвішування фігури.

Підвісити фігуру спочатку в одній точці (отворі); прокреслити олівцем лінію, яка співпадає з ниткою відвісу. Те ж саме повторити при підвішуванні фігури в іншій точці.

Зробити отвір в точці перетину проведених ліній – центра ваги фігури. Сумістити пластину (фігуру) з її зображенням на папері (виконану в однаковому масштабі). Центр ваги фігури знайдений аналітичним способом, центр ваги знайдений дослідним шляхом повинні співпадати.

Протокол 1.

№ з/п	Вид складної фігури та перелік її простих фігур	Площа фігури та її складових частин, мм^2	Координати центра ваги всієї фігури та її складових частин, мм
1	2	3	4	5
		А =	хс =	у с=
	I фігура –...	А1 =	х1 =	у 1 =
	ІІ фігура –...	А2 =	х2 =	у 2 =
	ІІІ фігура –...	А3 =	х3 =	у 3 =
	ІV фігура –...	А4 =	х4 =	у 4 =

ЗМІСТ ЗВІТУ

В звіті потрібно вказати мету роботи, обладнання, інструменти і матеріали; описати методику виконання розрахунків і проведення експериментального визначення центра ваги складної плоскої фігури згідно пунктів ходу виконання роботи; навести і заповнити таблицю протоколу 1; зробити висновки про результати роботи.

ХІД РОБОТИ

1.Згідно варіанту індивідуального завдання вибрати вихідні дані(табл. 3.2, рис.3.2).

2. Накреслити фігуру складної форми.

2.1. Вибрати масштаб побудови М1:2 (М1:1).

2.2. Розбити складну фігуру на прості і вказати центри ваги кожної.

2.3. Вибрати координатні вісі х0у.

3. Визначити координати центрів ваги кожної простої фігури: х_і; у _і (мм).

4. Обчислити площі кожної простої фігури А_і , мм² .

5. Обчислити координати центра ваги всієї фігури х_с і у _с за формулами (1), (2).

6. Провести експериментальну перевірку отриманих результатів:

а) навести схему установки для дослідного визначення координат центра тяжіння способом підвішування з описанням її будови та принципу дії;

б) зробити висновок про результати роботи.

7. Дати відповіді на контрольні запитання

ПРАВИЛА ТЕХНІКИ БЕЗПЕКИ

Кожен студент при роботі з обладнанням, інструментами та матеріалами зобов'язаний виконувати правила техніки безпеки, що встановлені інструкцією з охорони праці при виконанні робіт в кабінеті-лабораторії.

Про проходження інструктажу з питань охорони праці та безпеки життєдіяльності слід розписатися у відповідному журналі реєстрації інструктажів.

Таблиця 3.2. Індивідуальні завдання

№ варіанту	Розміри заданих фігур, см	№ схеми
a	b	c	d	e	f	m	n	h
1	2	3	4	5	6	7	8	9	10	11
1										1
2										2
3				-						3
4										4
5										5
6	-				-					6
7										1
8										2
9				-						3
10										4
11										5
12	-				-					6
13										1
14										2
15				-						3
16										4
17										5
18	-				-					6
19										1
20										2
21				-	2,5					3
22										4
23										5
24	-				-					6
25										1
26										2
27				-						3
28										4
29										5
30	-				-					6
Примітка трикутник рівносторонній круг і трикутник є вирізаними, як порожнини	Згідно рис. 3.2

Рис.3.2. Схеми складних фігур для індивідуальних завдань

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Чи можна вважати силу тяжіння тіла, як рівнодійну системи паралельних сил?

2. Чи може розміщуватись центр ваги поза тілом?

3. В чому доцільність експериментального визначення центра фігури?

4. Як визначається центр ваги складної фігури, яка складається з кількох простих фігур?

5. Як раціонально слід проводити розподіл складної фігури на прості частини при визначенні центра ваги всієї фігури?

6. Який знак має площа отворів (трикутників) в формулі для визначення центра ваги?

7. На перетині яких ліній трикутника знаходиться його центр ваги?

8. Якщо фігуру складно розділити на невелике число простих фігур, який спосіб визначення центра ваги може дати найбільш швидку відповідь?

Дата добавления: 2015-08-20