Дифференцирующие пассивные цепи.

Дифференцирующими называются четырехполюсники, мгновенные напряжения на выходе которых пропорциональны производной мгновенных напряжений на входе. В качестве пассивных дифференцирующих цепей на практике используют RC-цепи.

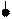
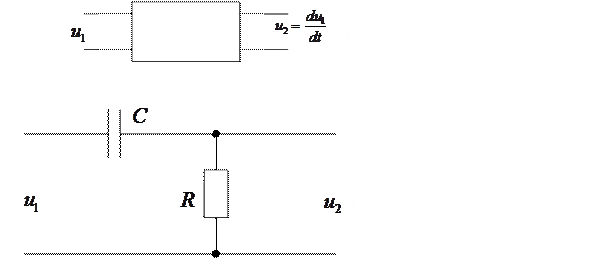
По второму закону Кирхгофа: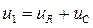

При 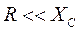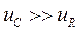в этом случае 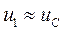, а 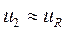. Ток в цепи с емкостью .

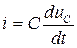Т.к. выходное напряжение снимается с сопротивления, определим зависимость напряжения на резисторе от входного напряжения.

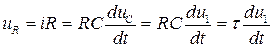, где 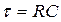- постоянная времени для RC- цепи.

Идеальное дифференцирование могло бы быть при 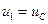, но это возможно лишь при 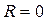. В этом случае 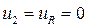, цепь при этом практически теряет смысл.

Вывод: Чем меньше R по сравнению с Х_С, тем ближе выходное напряжение к производной от входного, но тем меньше коэффициент передачи.

Идеальное дифференцирование невозможно, поэтому установим критерии практического дифференцирования:

1. , цепь становится практически дифференцирующей. Определим значение постоянной из условия дифференцирования

,

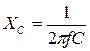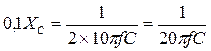
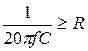, преобразуем неравенство 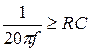, т.к. 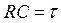, получаем .

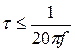Если постоянная времени цепи 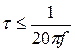, то для всех сигналов в диапазоне частот 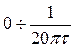, цепь является практически дифференцирующей.

2. 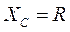, цепь является квазидифференцирующей (частично дифференцирующей). Это соблюдается при условии, что постоянная времени имеет такое значение, при котором коэффициент передачи 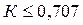. Существует частота, при которой цепь из дифференцирующей становится квазидифференцирующей. Эта частота называется граничной и зависит от величины постоянной времени

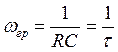, т.е. при значениях постоянной времени 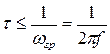, цепь является квазидифференцирующей.

3. 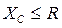, характер цепи приближается к резистивному, т.е. форма выходного напряжения будет приближаться к форме входного. При услови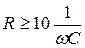и или 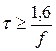цепь становиться разделительной.

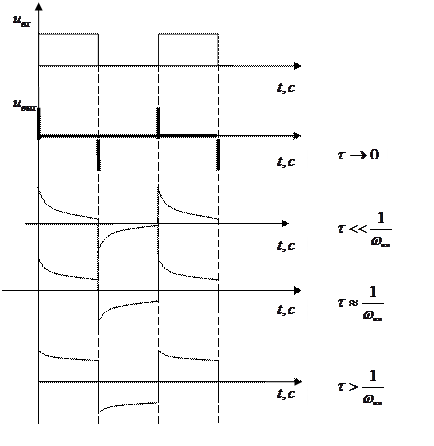
Вывод:

В зависимости от величины и соотношения резистивного и емкостного сопротивления, т.е. величины постоянной времени цепь может быть:

- практически дифференцирующей , ;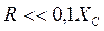

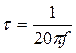-квазидифференцирующей , ;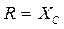

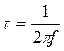-разделительной , .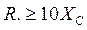

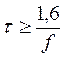Дата добавления: 2015-08-20