I. МЕТА РОБОТИ

Метою розрахунково-графічної роботиє закріплення та поглиблення отриманих теоретичних знань з дисципліни «Інформаційні технології у фармації» та використання їх на практиці; набуття практичних навичок застосування програмних засобів статистичної обробки даних, подання та аналізу їх результатів через виконання розрахунково-графічної роботи на тему «Статистична обробка даних за допомогою електронних таблиць».

IІ. АКТУАЛЬНІСТЬ РОБОТИ

Розвиток i впровадження інформаційних технологій (далі І.т.) у фармації є суттєвою складовою процесу інформати­зації державної галузі охорони здоров’я. Одним із сучасних прик­ладів застосування І.т. у фармацевтичній практиці є комп’ютерні системи управління­ реаліза­цією лікарських препаратів (далі ЛП). Такі системи покликані автоматизувати діяльність аптек, допомагаючи виконувати багато рутинних операцій і забезпечуючи функції з організації діяльності аптеки: безпосередній продаж ЛП та виробів медичного призначення; замовлення і закупівля ЛП у постачальників; проведення обліку; переоцінка і списання товарів та інше. При цьому системі необхідно збирати і зберігати статистичну інформацію про операції в процесі реа­лізації ЛП, а також проводити статистичну обробку цієї інформації. Для функціонування системи необ­хідна наявність таких баз даних: база даних товарів (ЛП) зі всіма їх характеристиками­ (найменування, лікарські форми, ціни, залишки на складі); база даних фірм (постачальників, замовників і партнерів) з їх реквізитами; база даних документів (накладних на прихід, вит­рату, списання товарів). Ця комп’ютерна система дозволяє легко виконувати такі практичні завдання, як пошук в базах даних, відстежувати оборот конк­ретного товару або групи товарів за певний період, проводити аналіз продажів препаратів­ за конкретний період. Окремо слід зазначити, що всі виконувані­ операції повинні відображатися в базі даних у реальному часі і бути доступними відразу­ всім користувачам аптечної комп’ютерної системи. Таким чином, комп’ютерну систему­ реалізації ЛП можна уявити собі як мере­жеву систему управління базами даних (СУБД). У цій системі можна проглянути інформацію про ціну за одиницю­ товару чи його залишки. Відповідні дані (чеки кожної покупки) зберігаються в базі даних комп’ютера, і на підставі цих даних формується статистика із загальної історії продажу.

Значення типу задач, які є предметом РГР полягає у тому, що вони дають можливість добиватися повноти статистичної інформації як за охопленням одиниць об'єкта, так і за комплексним відображенням усіх сторін процесу, що вивчається. Також дають можливість забезпечувати зіставлення статистичних показників за рахунок подібності вихідних даних, а також забезпечувати точність та надійність вихідної інфо­рмації для достовірності змісту процесу, що дослі­джується.

IІІ. ОБГРУНТУВАННЯ ВИБОРУ ЗАСОБІВ РОЗВ’ЯЗАННЯ ЗАДАЧІ І КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

Процесори електронних таблиць – це незмінний атрибут програмного забезпечення персонального комп’ютера. Електронна таблиця – це програма, що моделює на екрані двовимірну таблицю, яка складається з рядків і стовпців. Основним призначенням електронної таблиці є введення даних до комірок й обробка їх за формулами.

Електронна таблиця є універсальним засобом для автоматизації розрахунків над табличними даними. Її створюють у пам’яті комп’ютера, потім її можна переглянути, змінювати, записувати на магнітних та оптичних носіях для зберігання, друкувати на принтері.

Комірки електронних таблиць утворюються із рядків і стовпців, причому кожна з них має свою адресу. В комірок можна вводити як дані (числа, текст, логічні змінні), так і формули.

За допомогою табличних процесорів можна не тільки автоматизувати розрахунки, а й ефективно проаналізувати їхні можливі варіанти. Змінюючи значення одних даних, можна спостерігати за змінами інших, що залежать від них. Такі розрахунки виконуються швидко і без помилок, надаючи користувачу за лічені хвилини велику кількість варіантів розв’язання задачі.

Серед найвідоміших табличних процесорів є такі як: Excel, Quattro Pro. Досить велика перевага табличному процесору програми Excel. Можливості Excel набагато більші, ніж розуміють під терміном табличний процесор. Наприклад, використовуючи цю програму, на підприємстві можна розраховувати податки і заробітну плату, вести облік кадрів і витрат, планувати виробництво та керувати збутом. А потужні математичні та інженерні функції Excel дають змогу розв’язувати багато задач у галузі природничих та технічних наук.

Основні функції програми Excel:

· введення і редагування даних, автоматизація введення (автозаповнення, автозаміна тощо);

· форматування табличних даних із використанням стандартних засобів, стилів, шаблонів;

· виконання обчислень за формулами;

· аналіз табличних даних (введення проміжних і загальних підсумків, створення зведених таблиць, добір параметрів, прогнозування розв’язків);

· графічне зображення даних (побудова графіків, діаграм, уведення малюнків, відео матеріалів, географічних карт);

· робота зі списками (упорядкування й фільтрація записів, пошук даних);

· колективна робота з таблицями (обмін файлами в локальній мережі, спільне використання);

· обробка (статистичний аналіз) результатів експериментів;

· проведення однотипних складних розрахунків над великими наборами даних;

· автоматизація підсумкових обчислень;

· створення та аналіз баз даних (списків).

IV. ОПИС ПРОЦЕДУРИ РОЗВ’ЯЗАННЯ ЗАДАЧІ З КОРОТКИМИ ПОЯСНЕННЯМИ

1.1. Відкрити нову робочу книгу MS Excel. Підгодувати робочий аркуш для задачі за зразком, наведеним на рисунку 1. Присвоїти робочому аркушу ім’я «Точкові оцінки».

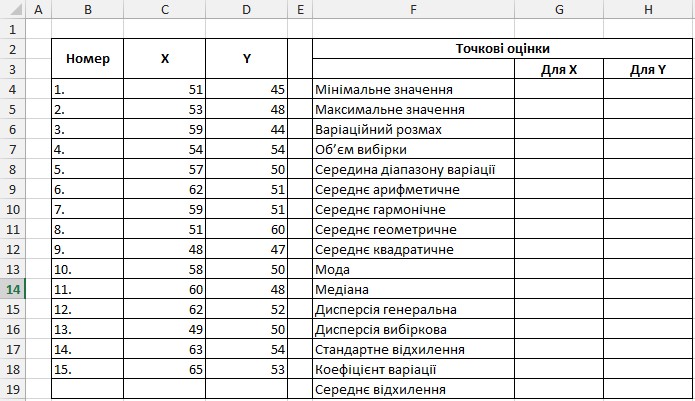
Рис.1 Зразок робочого аркуша для знаходження точкових оцінок.

1.2. Ввести розрахункові формули в комірки таблиці.

1.2.1. До комірки G4 ввести формулу для розрахунку мінімального значення X „=MIN(C:C)”. Це ж саме потрібно повторити і для Y, відповідно „=MIN(D:D)” в комірку H4.

1.2.2. До комірки G5 ввести формулу для розрахунку максимального значення X „=MAX(C:C)”. Це ж саме потрібно повторити і для Y, відповідно „=MAX(D:D)” в комірку H5.

1.2.3. До комірки G6 та H6 ввести формулу, для обчислення розмаху варіації, що являє собою різницю між найбільшим і найменшим значеннями її варіант, тобто: Xmax–Xmin.

Для Х вона матиме вигляд “=G5-G4” а для Y, відповідно “=H5-H4”.

1.2.4. В комірку G7 ввести формулу для знаходження об’єму вибірки X „=COUNT(C:C)”. Це ж саме потрібно повторити і для Y, відповідно „=COUNT(D:D)” в комірку H7.

1.2.5. До комірки G8 та H8 ввести формулу для розрахунку середини діапазону варіації X, як пів суми мінімального і максимального значень: (Xmax+Xmin)/2.

Для Х вона матиме вигляд “=(G4+G5)/2” а для Y, відповідно „=(H4+H5)/2”.

1.2.6. До комірки G9 та H9 ввести формулу, для обчислення середнього арифметичного: а=(a₁+a₂+...+а_n)/n.

Для Х вона матиме вигляд „=AVERAGE(C:C)” а для Y, відповідно „=AVERAGE(D:D)”.

1.2.7. До комірки G10 та H10 ввести формулу, для обчислення середнього гармонічного: .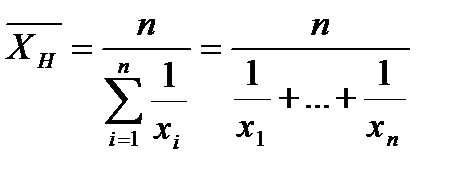

Для Х вона матиме вигляд „=HARMEAN(C:C)” а для Y, відповідно „=HARMEAN(D:D)”.

1.2.8. До комірки G11 та H11 ввести формулу, для обчислення середнього геометричного: .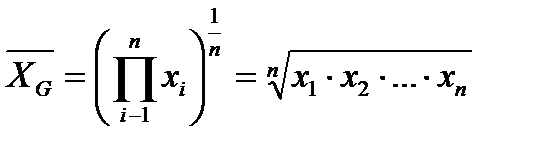

Для Х вона матиме вигляд „=GEOMEAN(C:C)” а для Y, відповідно „=GEOMEAN(D:D)”.

1.2.9. До комірки G12 та H12 ввести формулу, для обчислення середнього квадратичного: .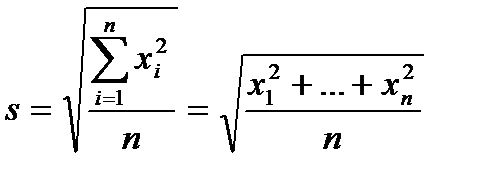

Для Х вона матиме вигляд „=SQRT(SUMSQ(C:C)/COUNT(C:C))” а для Y, відповідно „=SQRT(SUMSQ(C:C)/COUNT(D:D)”.

1.2.10. До комірки G13 та H13 ввести формулу, для обчислення моди:

.

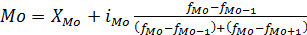Для Х вона матиме вигляд „=MODE(C:C))” а для Y, відповідно „=MODE(D:D)”.

1.2.11. До комірки G14 та H14 ввести формулу, для обчислення медіани: .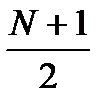

Для Х вона матиме вигляд „=MEDIAN(C:C)” а для Y, відповідно „=MEDIAN(D:D)”.

1.2.12. До комірки G15 та H15 ввести формулу, для обчислення генеральної дисперсії: .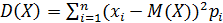

Для Х вона матиме вигляд „= VARPA(C:C)” а для Y, відповідно „= VARPA(D:D)”.

1.2.13. До комірки G16 та H16 ввести формулу, для обчислення вибіркової дисперсії: .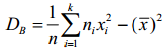

Для Х вона матиме вигляд „=VARP(C:C)” а для Y, відповідно „=VARP(D:D)”.

1.2.14. До комірки G17 та H17 ввести формулу, для обчислення стандартного відхилення: .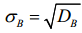

Для Х вона матиме вигляд „=STDEV(C:C)” а для Y, відповідно „=STDEV(D:D)”.

1.2.15. До комірки G19 та H19 ввести формулу, для обчислення середнього відхилення: .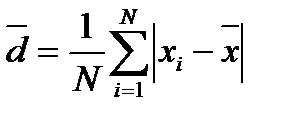

Для Х вона матиме вигляд „=AVEDEV(C:C)” а для Y, відповідно „=AVEDEV(D:D)”.

1.2.16. До комірки G18 та H18 ввести формулу, для обчислення коефіцієнту варіації, що є відношенням стандартного відхилення до вибіркового середнього:

.

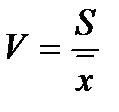Для Х вона матиме вигляд „=G17/G9” а для Y, відповідно „=H17/H19”.

Завдання виконано, скріншот вікна програми з усіма формулами на рисунку 2.

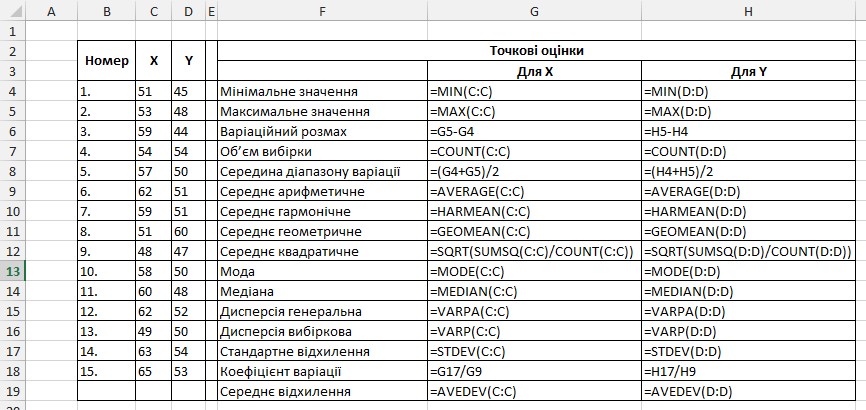
Рис.2 Скріншот вікна програми з усіма функціями

1.3. Перейти на новий робочий аркуш MS Excel. Підгодувати робочий аркуш присвоївши йому ім’я «Середні значення величин». На попередньому аркуші «Точкові оцінки» обрати максимальні та мінімальні значення а також усі середні значення величин.

1.4. Створення діаграми середніх значень для величин X та Y.

1.4.1. Виділити потрібні точкові оцінки для Х та перейти в розділ «Вставлення» далі «Рекомендовані діаграми».

1.4.2. У майстрі вставлення діаграм обрати «Звичайна стовпчаста діаграма» та натиснути «ОК».

1.4.3. Налаштувати діаграму додавши такі елементи як: назва діаграми, сітка підписи даних а також лінію тренду, для зображення середніх значень величин. Це ж повторити і для Y. Після всіх маніпуляцій діаграми виглядатимуть так, як на рисунку 3.

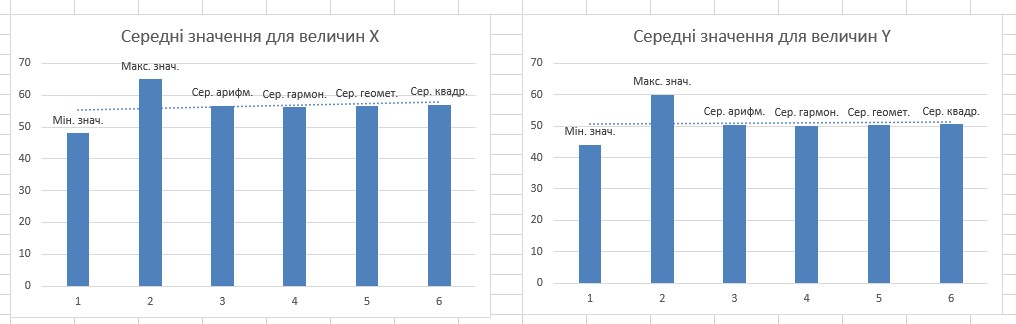
Рис.3 Середні значення величин за допомогою діаграми

1.5. Перейти на новий робочий аркуш MS Excel. Підгодувати його скопіювавши у комірки першого та другого рядка значення елементів заданої вибірки для X та Y з першого завдання. Присвоїти робочому аркушу ім’я «Кореляційне поле».

1.6. Створити кореляційне поле для величин X та Y.

Для побудови кореляційного поля необхідно застосовувати діаграму типу «Точкова», яка призначена саме для відображення пар значень. Діаграми інших типів для цієї мети не підходять, оскільки не забезпечують відображення зв’язаних пар значень.

1.6.1. Виділити значення Х та Y, тоді перейти в розділ «Вставлення» далі «Усі діаграми», після чого обрати «Точкова» і вибираємо «Точкова діаграма із прямими лініями та маркерами».

1.6.2. Налаштувати діаграму додавши такі елементи як: осі, та їх назви, назву діаграми, сітка, тощо. Після всіх маніпуляцій діаграма виглядатиме так, як на рисунку 4.

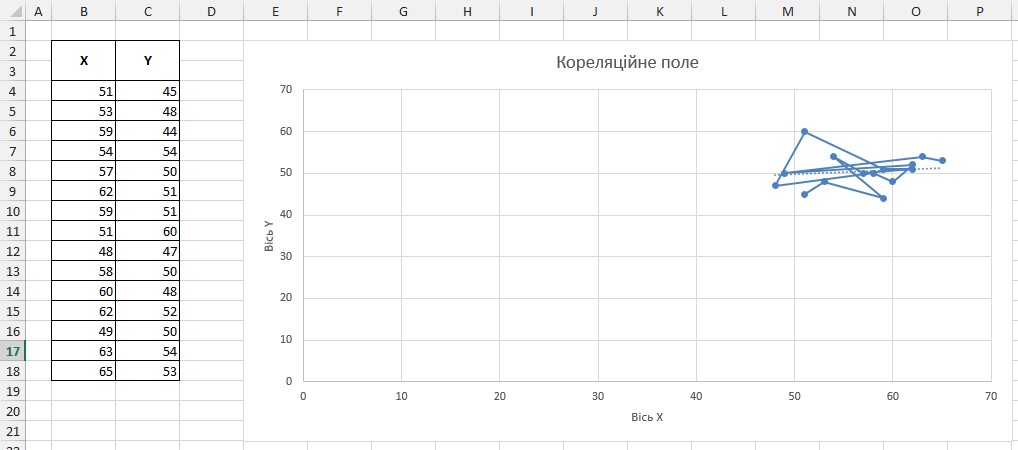
Рис.4 Кореляційне поле

1.7. Перейти на новий робочий аркуш MS Excel. Підгодувати робочий аркуш для задачі за зразком, наведеним на рисунку 5. Присвоїти робочому аркушу ім’я «Коефіцієнт кореляції».

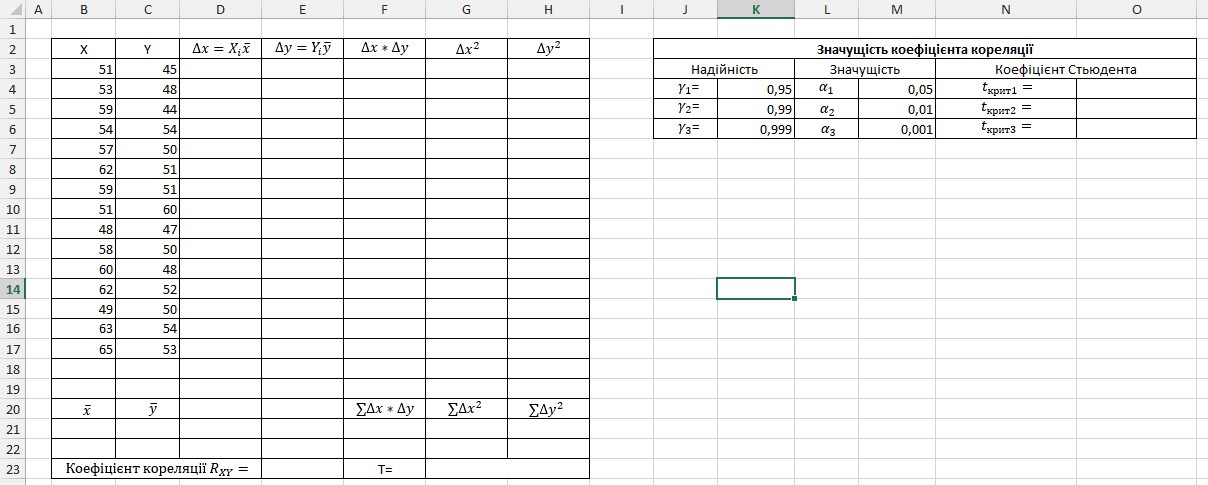
Рис.5 Зразок робочого аркуша для знаходження коефіцієнта кореляції

1.8. Ввести розрахункові формули в комірки таблиці.

1.8.1. У комірку D3 ввести формулу для розрахунку відхилення х_i від 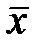, 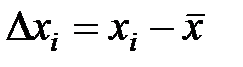. В Excel вона виглядатиме: („=B3-$B$21”), а у комірку E3 – для розрахунку відхилення у_і від 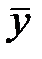, яка виглядатиме: („=C3-$C$21”). Розтягнути введені формули на відповідні діапазони D3:D17 та E3:E17.

1.8.2. У комірках F3, G3, H3 створити формули для розрахунку відповідно: добутку відхилень вибіркових значень ∆x_i∙∆y_i в Excel вона виглядатиме: „=D3*E3”; квадрату відхилення ∆х - „=D3^2”, квадрату відхилення ∆у - „=E3^2”. Створені формули розтягнути на відповідні діапазони: F3:F17; G3:G17 та H3:H17.

1.8.3. У комірки F21, G21, H21 ввести формули для обчислення сум: 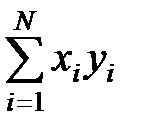в Excel вона виглядатиме: „=SUM(F3:F17)”, 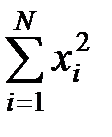- „=SUM(G3:G17)” а також 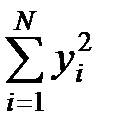- „=SUM(H3:H17)”.

1.8.4. До комірки E23 ввести формулу для розрахунку коефіцієнта кореляції (коефіцієнт кореляції Пірсона):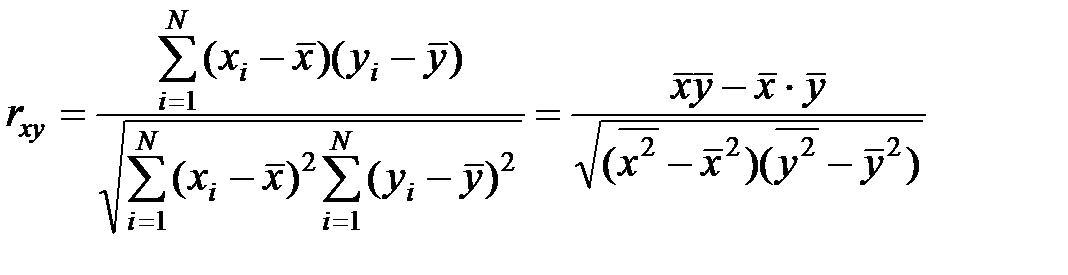

В Excel вона виглядатиме: “=F21/SQRT(G21*H21)”.

1.8.5. До комірки G23 ввести формулу для розрахунку критерію значущості коефіцієнта кореляції: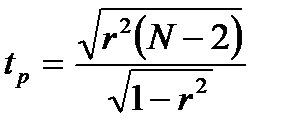

В Excel вона виглядатиме: «=SQRT(E23^2)*(COUNT(B3:B17)-2)/(1-E23^2)».

1.8.6. До комірок O4, O5, O6 ввести формули для знаходження критичного значення критерію, яке визначають за розподілом Стьюдента при заданій значущості α і числі ступенів свободи ν = N – 2: .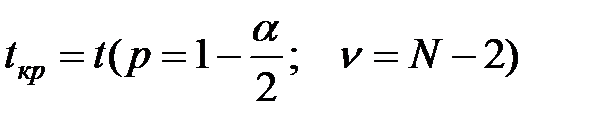

Для цього потрібно обрати комірку O4 і ввести формулу „=TINV(1-K4;COUNT($B$3:$B$17)-2)” а потім скопіювати формулу з комірки O4 на комірки O5 i O6. У кінці маємо отримати результат, як на рисунку 6 та 7.

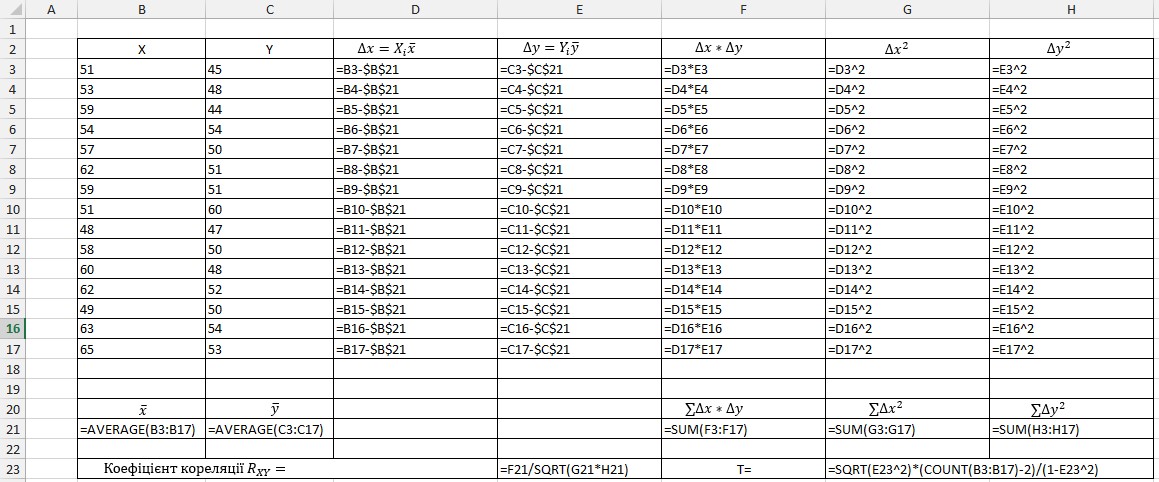
Рис.6 Формули першої таблиці

Рис.7 Формули другої таблиці

1.9. Відкрити нову робочу книгу MS Excel. Підгодувати робочий аркуш для задачі за зразком, наведеним на рисунку 8. Присвоїти робочому аркушу ім’я «Регресія».

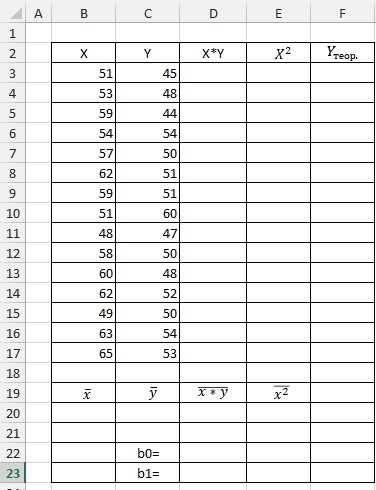
Рис.8 Зразок створення таблиці

1.10. Ввести розрахункові формули в комірки таблиці.

1.10.1. До комірки D3 ввести формулу, для обчислення добутку відповідних елементів вибірок: X*Y. У Excel вона матиме вигляд: „=B3*C3”, після чого розтягнути формулу на діапазон D3:D17.

1.10.2. До комірки E3 ввести формулу, для обчислення квадрату елементів вибірки X. У Excel вона матиме вигляд: „=B3^2”, після чого розтягнути формулу на діапазон E3:E17.

1.10.3. До комірки D18 ввести формулу для обчислення середнього значення добутку x_i∙y_i за допомогою функції “=AVERAGE(D3:D17)”.

1.10.4. До комірки E20 ввести формулу для розрахунку середнього значення квадрату елементів вибірки, яка буде мати вигляд “=AVERAGE(E3:E17)”.

1.10.5. До комірки D23 занести формулу для обчислення коефіцієнта регресії b₁:

.

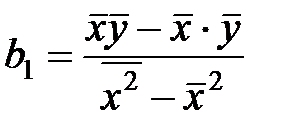В Excel вона виглядатиме: «=(D20-B20*C20)/(E20-B20*B20)», а до комірки D22 – формулу для обчислення коефіцієнта b₀ (вільного члена рівняння регресії):

.

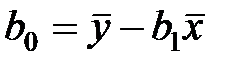Яка в Excel виглядатиме так: «=C20-D23*B20»

1.10.6. До комірки F3 ввести формулу рівняння регресії, яка буде мати вигляд «=$D$23*B3+$D$22». Далі потрібно скопіювати формулу комірки F3 на діапазон F3:F17. Результат виконання завдання на рисунку 9.

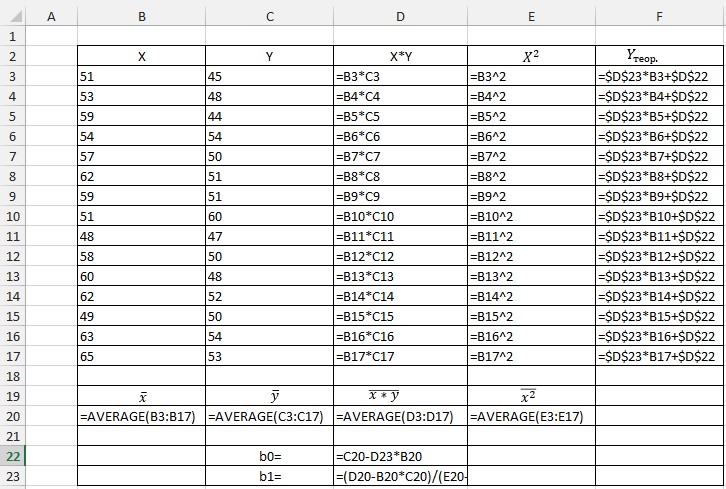
Рис.9. Результат створення таблиці

1.11. Побудувати кореляційне поле з лінією регресії.

1.11.1. Виділити на робочому аркушеві «Регресія» діапазони B3:C17 і F3:F17 (несуміжні діапазони виділяються протягуванням вказівника при натисненні лівої кнопки миші і клавіші CTRL).

1.11.2. Викликати майстра діаграм і обрати діаграму типу «Точкова» з маркерами і прямими відрізками.

1.16.3. Виконати налаштування діаграми (назва, осі тощо). Після налаштування діаграма матиме такий вигляд, як на рисунку 10.

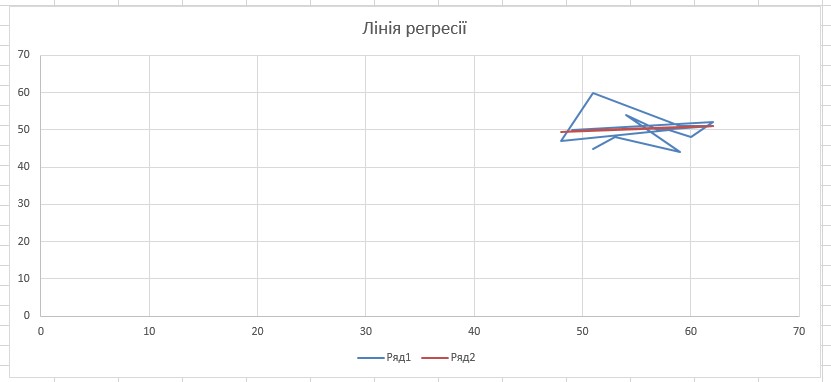
Рис.10 Діаграма лінії регресії

Дата добавления: 2015-08-20