
Читайте также:
|
Подставляем в уравнение равновесия
 =0
=0
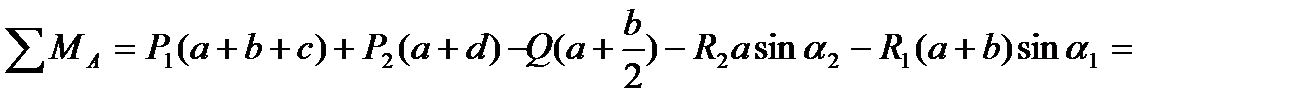 10*10^3(6+5+1)-40*10^3(6+2.5)-20*10^3*5(6+2.5)+52.5*10^3*1+72.9*10^3(6+5)*1=0
10*10^3(6+5+1)-40*10^3(6+2.5)-20*10^3*5(6+2.5)+52.5*10^3*1+72.9*10^3(6+5)*1=0
2.Вычислим напряжения, возникающие при неточности изготовления элементов конструкции, т. е
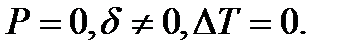

Рисунок3
Второй стержень был изготовлен на 0,002  длиннее номинальной длины. При сборке конструкции в стержнях появятся монтажные напряжения. Расчетная схема будет выглядеть, как показано на Рисунке3.
длиннее номинальной длины. При сборке конструкции в стержнях появятся монтажные напряжения. Расчетная схема будет выглядеть, как показано на Рисунке3.
На Рисуеке3 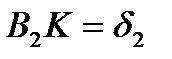 ;
;


 и
и  - монтажные напряжения.
- монтажные напряжения.
1)Уравнение равновесия для рассматриваемого случая имеет следующий вид:
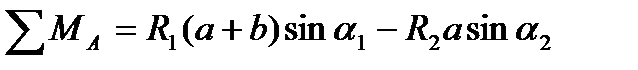 =0;
=0;
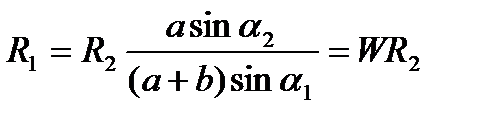 (1);
(1);
2)Система один раз статически неопределима, т.е К=1.
3)Составим уравнение совместимости деформации.
Из  :
: 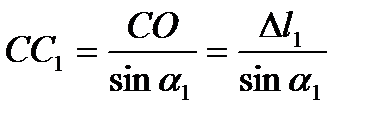 (2);
(2);
Рассмотрим  и
и  :
: 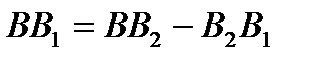 ,
,
где  и
и 

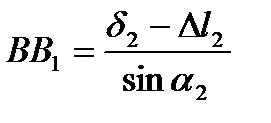 ;
;
Из подобия  и
и 



По закону Гука:
 и
и 

 , т.к
, т.к  и
и 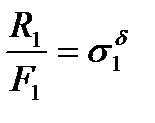 , То выражения (2) и (1) примут вид соответственно
, То выражения (2) и (1) примут вид соответственно
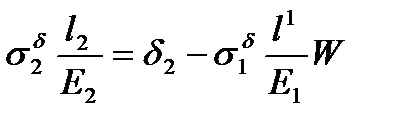 (3) и
(3) и
 ,разделим обе части данного выражения на
,разделим обе части данного выражения на  ,получим
,получим
 (4).
(4).
4)Решим систему из уравнений (4) и (3):





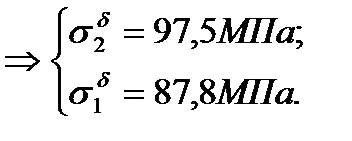 Т.к оба стержня сжимаются,
Т.к оба стержня сжимаются,
то окончательно получим  и
и  .
.
Проверка: 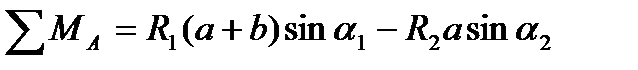 =0
=0
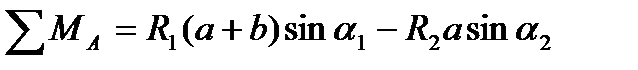 =
=
3.Рассчитаем температурные напряжения, т.е.


Рисунок4
 укорочение второго стержня составит
укорочение второго стержня составит  . При сборке стержень займет промежуточное положение и его упругое удлинение будет соответствовать отрезку
. При сборке стержень займет промежуточное положение и его упругое удлинение будет соответствовать отрезку 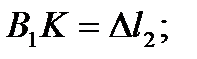

1)Составим уравнение равновесия:
 =0
=0
 (1)
(1)
2)Система один раз статически неопределима, т.е К=1.
3) Составим уравнение совместимости деформации.
Из 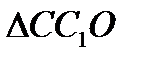 :
:  ;
;
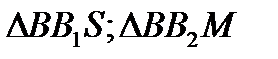 и
и 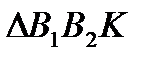 :
:  .
.
Рассмотрим  и
и  . Они подобны
. Они подобны 
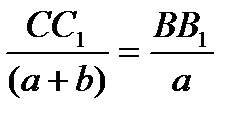 ;
;
 ,
,

По закону Гука:
 и
и 

 (2), т.к
(2), т.к 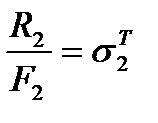 и
и  ,
,
то выражения (2) и (1) примут вид соответственно
 (3) и
(3) и
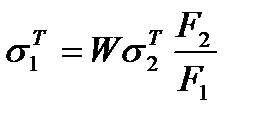 (4)
(4)
4)Решим систему из уравнений (3) и (4):








 Т.к оба стержня растягиваются,
Т.к оба стержня растягиваются,
то окончательные результаты: 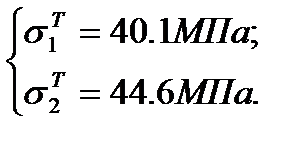
Проверка:
Дата добавления: 2015-08-20; просмотров: 37 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Рассмотрим как будет деформироваться система под действием сил Р и q, т.е | | | Подбор сечений элементов систем |