Электрический ток

Электрическим током называется движение электрических зарядов (электронов в металлах, электронов и ионов в жидкостях и газах) под действием электрического поля.

Движение положительных зарядов по полю эквивалентно движению отрицательных зарядов против поля.

За направление тока принято направление положительного заряда.

Условия существования электрического тока (в дальнейшем просто тока в проводнике):

а) наличие свободных заряженных частиц;

б) наличие электрического поля (разности потенциалов на концах проводника).

Действия электрического тока:

а) ТЕПЛОВОЕ – нагревание проводника, по которому идет ток;

б) ХИМИЧЕСКОЕ – изменение химического состава проводника (электролиз и сопутствующие ему явления);

в) МАГНИТНОЕ – силовое воздействие на другие проводники с током и намагниченные тела (магнетики).

Основные характеристики электрического тока:

а) сила тока I – численно равна количеству электричества (заряду) Q, протекающего по проводнику за время t: I = dq / dt. Измеряется в амперах (А) – амперметром.

В зависимости от величины и направления токи бывают: постоянные, переменные, пульсирующие и другие. Будем рассматривать только постоянные токи I = const.

Ток измеряется прибором – амперметром, который включается в цепь последовательно проводнику (сопротивлению).

б) напряжение U – равно разности потенциалов на участке цепи.

Напряжение измеряется прибором – вольтметром, который включается параллельно проводнику (сопротивлению);

в) сопротивление R проводника.

Сопротивление зависит:

1. От длины проводника ℓ, его сечения S и материала (характеризуется удельным сопротивлением проводника ρ): 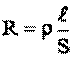Сопротивление измеряется в омах (Ом) – омметром.

2. От температуры t°С (илиТ): R = R₀ (1+ αt), где R₀ – сопротивление проводника при 0°С,

α – температурный коэффициент сопротивления.

3. Проводники могут соединяться последовательно и параллельно.

Соединение	Последовательное	Параллельное
Сохраняющаяся величина	I1 = I2 = … = In I = const	U1 = U2 = …Un U = const
Суммируемая величина	напряжение	cила тока
Результирующее сопротивление

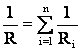
г) плотность тока j – физическая величина, определяемая силой тока I проходящего через единицу площади поперечного сечения S проводника: j = =

д) электрическая сила (ЭДС) ε – физическая величина, определяемая работой сторонних (неэлектрических) сил А_ст по перемещению единичного положительного заряда q:

Если в цепи на носители тока действуют силы электрического поля, то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способно создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.

Источники тока также можно соединить последовательно и параллельно:

1. При последовательном соединении источников:

ε_посл = ε·n,

r_посл = r·n, где ε – ЭДС одного источника, r – сопротивление одного источника, n – число источников.

2. При параллельном соединении n одинаковых источников:

ε_пар = ε,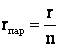

Элементы электрических цепей и сами электрические цепи изображают схематически следующим образом:

	– внешнее сопротивление проводника (участок электрической цепи без ЭДС)
	– амперметр и его включение в цепь;
	– вольтметр и его включение в цепь;
	– источник тока (источник ЭДС) с внутренним сопротивлением.
	– последовательное соединение сопротивлений и источников тока.
	– параллельное соединение сопротивлений и источников тока.
	– полная электрическая цепь.

Для решения задач по расчету электрических цепей используется закон Ома:

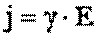1. Закон Ома для участка цепи (без ЭДС): или , где 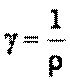– удельная проводимость проводника,

Е – напряженность электрического поля в проводнике.

2. Закон Ома для полной цепи: где R – внешнее сопротивление цепи, r – внутреннее сопротивление источника тока, R + r – называется полным сопротивлением цепи.

Следствия:

а) если R → 0, источник замкнут накоротко:

где I_кз – ток короткого замыкания;

б) если R → ∞, цепь разомкнута:

I = 0; U = ε, т.е. ЭДС источника численно равна напряжению на его зажимах при разомкнутой внешней цепи.

Для расчетов полных электрических цепей полезно знать следующие величины:

а) полная мощность, развиваемая источником: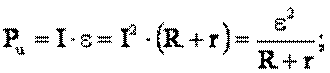

б) полезная мощность (выделяемая на внешнем сопротивлении):

в) мощность потерь: P_потерь = P_u – P_n = I²·r;

г) КПД источника:

Электрический ток I, проходя по участку цепи без ЭДС с сопротивлением R, совершает работу А по перемещению электрических зарядов, которую можно рассчитать по формуле: 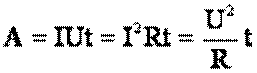, где U – напряжение на участке цепи, t – время пропускания тока.

Мощность N тока, согласно определения, равна:

При протекании тока по проводнику он нагревается и в нем выделяется количество теплоты Q, которое без учета потерь рассчитывается по закону Джоуля-Ленца: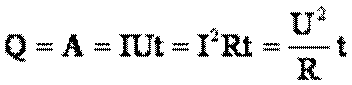

Задача №1. Имеется моток медной проволоки, площадь поперечного сечения которой S = 0,10 мм². Масса всей проволоки m = 0,30 кг. Определить сопротивление проволоки. Удельное сопротивление меди, плотность Д = 8,9·10³ кг/м³.

S = 0,10 мм² = 1·10^-7 м²; m = 0,30 кг; ρ = 0,017·10^-6 Ом·м; Д = 8,9·10³ кг/м³.

R –?

Решение: сопротивление проволоки длинной ℓ: 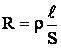(1)

Масса проволоки: m = ДℓS, где Д – плотность.

Отсюда . Подставив эти значения в формулу (1), найдем R: ;

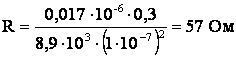
Ответ: сопротивление мотка проволоки равно 57 Ом.

Задача №2. Амперметр, предназначенный для измерения силы тока не более I_а = 20 мА, необходимо использовать для измерения силы тока до I = 0,5 А. Рассчитать сопротивление шунта R_ш, если сопротивление амперметра R_а = 5 Ом.

Iа = 20 мА = 2·10^-2 А; I = 0,5 А; Rа = 5 Ом.
Rш –?

Решение: если в цепи сила тока больше максимальной I_а, на которую рассчитан амперметр, то параллельно ему включается резистор (шунт), как показано на рисунке.

При этом ток силой I в цепи частично ответвляется в шунт:

I = I_а + I_ш,

где I_а, I_ш – силы токов, идущих через амперметр и шунт.

Пусть сила тока в цепи I = n·I_а, т.е. в n раз больше I_а. Тогда через шунт идет ток силой:

I_ш = I – I_а = n·I_а – I_а = (n – 1).

Напряжение на амперметре и шунте одинаковые: I_аR_а = I_шR_ш. Отсюда:

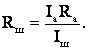Следовательно 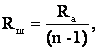где

Подсчитав числовые значения, найдем R_ш:

. Ответ: сопротивление шунта равно 0,2 Ом.

Задача №3. Вольтметр, рассчитанный на измерение напряжений до U_в = 30 В, имеет внутреннее сопротивление R_д добавочного резистора, который нужно подключить к вольтметру, чтобы им можно было измерять напряжение до U = 300 В.

Uв = 30 В; Rв = 3 кОм = 3·10^3 Ом; U = 300 В.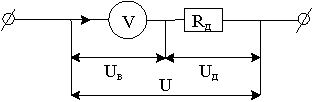
Rд –?

Решение: если измеряемое напряжение больше максимального U_в, на которое рассчитан вольтметр, то можно последовательно с ним включить добавочный резистор (рис.). Пусть R_в – сопротивление вольтметра, R_д – сопротивление добавочного резистора, U_в – предел измерения вольтметра, U= n·U_в – измеряемое напряжение, в n раз больше допустимого. Поскольку вольтметр и добавочный резистор соединены последовательно, то: U = U_в + U_д отсюда U_д = U – U_в = n U_в – U_в = U_в(n – 1).

Сила тока, проходящего через вольтметр и добавочный резистор, одна и та же. Поэтому, используя закон Ома для участка цепи, будем иметь:

откуда R_д = R_в·(n –1) = 27·10³ Ом = 27 кОм.

Ответ: добавочное сопротивление равно 27 кОм.

Задача №4. При температуре t₁ = 20°C сопротивление платиновой проволоки R₁ = 20 Ом, а при температуре t₂ = 500°C, R₂ = 59 Ом. Найти значение температурного коэффициента сопротивления платины.

t₁ = 20°C; R₁ = 20 Ом; t₂ = 500°C; R₂ = 59 Ом.

α –?

Решение: выражения для сопротивления проволоки при температурах t₁ и t₂ имеют соответственно вид:

R₁ = R₀·(1 + α t₁),

R₂ = R₀·(1 + α t₂),

где R₀ – сопротивление проволоки при 0°C;

α – температурный коэффициент сопротивления.

Разделив почленно первое равенство на второе, получим:

Отсюда: , α = 4,4·10^-3 градус^-1

Ответ: температурный коэффициент сопротивления платины 4,4·10^-3 градус^-1.

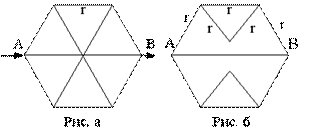Задача №5. Из отрезков проволоки с одинаковым сопротивлением составлена фигура, изображенная на рис. a. Она включена в цепь точками А и В. Вычислить сопротивление фигуры.

Решение: заданную фигуру можно представить состоящей из трех отдельных ветвей – такая эквивалентная схема изображена на рис. б. Сопротивление R₁ верхней ветви равно:

Очевидно, оно в точности равно сопротивлению нижней ветви: R₁ = R₂. Сопротивление центральной ветви: R₂ = 2·r

Все ветви соединены параллельно, поэтому их общее сопротивление будет:

Задача №6. Три одинаковых сопротивления по R Ом каждое соединены последовательно в цепь (рис. а). Изменится ли сопротивление между концами А и D цепи, если точки А и С, В и D замкнуть накоротко?

Решение: эквивалентная схема того, что получилось после замыкания, изображена на рис. б. Сразу видно, что из последовательного получилось параллельное соединение проводников. Если до замыкания сопротивление между точками А и D было 3R, то после замыкания оно стало , т.е. уменьшилось в девять раз. Ответ: да, уменьшилось в 9 раз.

Задача №7. Батарея аккумуляторов с э.д.с. ε = 6 В и внутренним сопротивлением r = 1,4 Ом питает внешнюю цепь, состоящую из двух параллельных сопротивлений R₁ = 2 Ом и R₂ = 8 Ом. Определить разность потенциалов U на зажимах батареи и силы токов I₁ и I₂ в сопротивлениях.

ε = 6 В; r = 1,4 Oм; R₁ = 2 Ом; R₂ = 8 Ом.

U, I₁, I₂ –?

Решение: сопротивление внешней цепи: 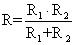R = 1,6 Ом.

Общую силу тока во внешней цепи найдем из закона Ома для полной цепи:

Падение напряжения во внешней цепи: U = I·R = 2·1,6 = 3,2 В

Силы тока в сопротивлениях равны:

Ответ: разность потенциалов на зажимах батареи 3,2 В, а силы токов в сопротивлениях 1,6 А и 0,4 А.

Задача №8. Элемент с э.д.с. ε = 1,1 В и внутренним сопротивлением r = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить: 1) силу тока в цепи I; 2) падение потенциала U₁ во внешней цепи; 3) падение потенциала U внутри элемента; 4) К.П.Д. (η) элемента?

ε = 1,1 В; r = 1 Ом; R = 9 Ом.

I, U₁, U, η –?

Решение: согласно закону Ома для замкнутой цепи:

Падение потенциала во внешней цепи: U = IR; U = 0,11 A·9 Ом = 0,99 В.

Падение потенциала внутри элемента: U₁ = Ir; U₁ = 0,11A·1 Ом = 0,11 В.

Коэффициент полезного действия элемента:

Ответ: I = 0,11 A; U = 0,99 B; U₁ = 0,11 B; η = 0,9.

Задача №9. Батарея элементов с э.д.с. ε = 6 В при замыкании на внешнее сопротивление 1 Ом дает ток силой I = 3 А. Какова будет сила тока I_к.з. при коротком замыкании батарей?

ε = 6 В; I = 3 A; R = 1 Ом.

I_к.з –?

Решение: из закона Ома для замкнутой цепи:

Найдем внутреннее сопротивление батарей: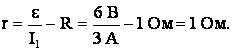

Так как при коротком замыкании R → 0, то сила тока короткого замыкания будет равна:

Ответ: ток короткого замыкания равен 6А.

Задача №10. Несколько источников тока соединены так, как показано на рисунке. Каковы показания амперметра и вольтметра? Сопротивление вольтметра считать бесконечно большим. Сопротивлением амперметра и соединительных проводов пренебречь. Рассмотреть два случая: когда все источники тока одинаковы и когда они имеют различные ЭДС и различные сопротивления.

Решение: если все n источников одинаковые, то сила тока в цепи:

.

Таково показание амперметра.

Как следует из закона Ома для замкнутой цепи, вольтметр покажет напряжение: U = ε – I·r.

Подставив сюда значение силы тока, получим U = 0.

Если все источники различны, то сила тока в цепи: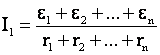

В этом случае вольтметр покажет U₁ ≠ 0.

Задача №11. Электровоз движется со скоростью V = 36 км/ч и развивает в среднем силу тяги F = 5∙10⁴ Н. Найти ток, проходящий через мотор электровоза (без учета потерь), если напряжение на нем U = 500 В.

V = 36 км/ч = 10 м/с; F = 5∙10⁴ H; U = 500 B.

I –?

Решение: на основании закона сохранения энергии механическая работа, совершаемая электровозом, равна работе электрического тока, протекающего через мотор электровоза: IUt = A, где I – сила тока,

t – время.

Это равенство можно переписать следующим образом: 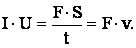где F – сила тяги,

S – путь, пройденный электровозом за время t, v – скорость электровоза.

Искомый ток ; ;

. Ответ: ток, протекающий через мотор электровоза равен 1000А.

Задача №12. Электрический чайник имеет две обмотки. При включении одной из них чайник вскипает через 10 мин, при включении другой – через 15 мин. Через сколько времени чайник вскипит, если обмотки включить вместе: а) параллельно, б) последовательно.

Решение: для того чтобы вскипятить чайник требуется энергии W. Эта энергия выделяется при нагревании обмоток электрическим током (пренебрегая рассеиванием тепла в окружающее пространство). Если включить первую обмотку, то W = 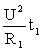откуда R = ,

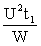где U – напряжение сети, R₁ – сопротивление первой обмотки, t₁ – время, за которое чайник вскипает при включении первой обмотки.

Аналогично, если включить вторую обмотку: , получаем R = .

Соединим теперь обмотки параллельно. Энергия W теперь выделяется при нагревании обеих обмоток. Поскольку напряжение на обеих обмотках равно U, то

где t₃ – время, за которое чайник вскипает при параллельном соединении обмоток.

Решая совместно уравнения, получим:

Пусть теперь обмотки соединены последовательно. В этом случае:

Решая совместно уравнения, получим: t₄ = t₁ + t₂ = 5 мин

Расчет производился во внесистемных единицах.

Ответ: при параллельном соединении время закипания чайника больше на 1 мин (t₃ = 6 мин, t₄ = 5 мин).

Задача №13. Источник тока замыкается один раз проводником с сопротивлением 4 Ом, другой раз – с сопротивлением 9 Ом. В обеих случаях количество теплоты, выделившейся в проводниках за одно и тоже время, оказалось одинаковым. Определите внутреннее сопротивление источника.

R₁ = 4 Ом; R₂ = 9 Ом; P₁ = P₂ = P.

r –?

Решение: согласно закону Джоуля-Ленца и условию задачи: (1)

Согласно закону Ома для замкнутой цепи имеем: (2) (3)

Поделив (2) на (3) и используя (1), получим: (4)

Решив (4) относительно r, будем иметь: 3R₁ + 3r = 2R₂ +2r, Откуда r = 2R₂ – 3R₁ = (18 – 12) = 6 Ом

Ответ: Внутреннее сопротивление источника 6 Ом.

Дата добавления: 2015-08-20