Вычисление производной функции

В MathCAD встроены процедуры для численного определения производных функции в заданной точке. Для вычисления производной первого порядка служит оператор дифференцирования, ввод которого можно выполнить нажатием кнопки панели Исчисление (Calculus ) или комбинацией двух клавиш Shift и?

Задача 3. Вычислить производную функции в точке .

Рис. 2. Вычисление производной функции в заданной точке в среде MathCAD

Чтобы вычислить производную порядка выше первого, можно последовательно применить несколько раз оператор дифференцирования. Например,

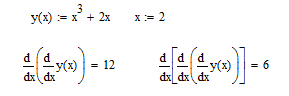
Рис.3 Вычисление производной порядка выше первого с последовательным применением оператора дифференцирования

Однако лучше воспользоваться оператором дифференцирования n-го порядка 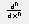, вводимого нажатием кнопки панели инструментов Исчисление (Calculus ) или комбинацией клавиш Ctrl+Shift+?

Заметим, что при заполнении любого из двух знакомест для ввода порядка производной автоматически заполняется второе знакоместо.

Теперь предыдущие вычисления можно оформить так:

Рис.4 Вычисление производной порядка выше первого с применением оператора дифференцирования n-го порядка

Задача 4. Вычислить производные 2-го и 3-его порядка функции в точке двумя описанными выше способами.

Однако если требуется вычислить производную порядка выше 5, то придется последовательно применить несколько раз оператор дифференцирования n-го порядка.

Например, найдем производную 7-го порядка функции

Задача 5. Вычислить производную 7-го порядка функции в точке .

Рис.4 Вычисление производной 7-го порядка с последовательным применением оператора дифференцирования n-го порядка

Дата добавления: 2015-08-18