| |
|
|
|
| | Решите задачу
| Решите задачу
| Решите задачу
|
| *
| Длины образующей и диаметра основания конуса равны соответственно 26 см и 20 см. Через середину образующей конуса проведена плоскость параллельная плоскости основания. Найти высоту полученного усеченного конуса.
| Длина образующей усеченного конуса 12 см. Длины окружностей его оснований 14П см и 30П см. Найти угол между образующей
и плоскостью основания усеченного конуса
| Осевое сечение цилиндра – квадрат, площадь которого 36 дм2. Вычислить длину образующей и площадь основания цилиндра.
|
|
| Прямоугольник диагональ которого равна 25 см, а одна сторона 20 см вращается вокруг меньшей стороны. Вычислить длину высоты полученного цилиндра и площадь его основания.
| Длины радиусов оснований и образующий усеченного конуса равен соответственно 7 см.,15 см. и 17 см.Найти высоту конуса.
| Угол между двумя радиусами шара 90º.Расстояние между их концами 15 см. Найти расстояние по поверхности шара между концами радиусов.
|
|
| Осевое сечение цилиндра – квадрат, диагональ которого 12 см. Вычислить длину образующей и площадь основания цилиндра.
| Диаметр шара 52 см. Вычислить площадь сечения шара плоскостью, удаленной от его центра на 10 см..
| Точка С сферы удалена от концов его диаметра – АВ на 10 см и 24 см. Вычислить длину линии пересечения сферы и плоскости содержащей точки А,В и С.
|
|
| Диагональ прямоугольника 18 см, она составляет с его стороной угол 30º. Прямоугольник вращается большей стороны. Вычислить высоту и площадь основания полученного цилиндра.
| Длины радиусов оснований усеченного конуса 10 см и 8 см. Угол между образующей и плоскостью основания 45º. Вычислить площадь осевого сечения усеченного конуса.
| На поверхности шара даны три точки, расстояние между которыми равны 8 см. Вычислить площадь сечения шара плоскостью содержащей эти точки.
|
|
| Высота цилиндра на 2 см больше радиуса его основания. Площадь осевого сечения цилиндра 96 см2. Найти радиус основания и высоту цилиндра.
| Длины радиусов оснований и высота конуса равны соответственно 4 дм, 20 дм и 30 дм. Найти длину образующей этого усеченного конуса.
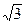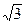| Радиус сферы 10 см. На расстоянии 5  см от ее центра проведена плоскость. Вычислить длину линии их пересечения.
|
