Linear multiple variables regression

The average square deflection of variables:

;

;

.

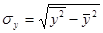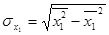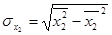Coefficients of correlation for two variables regression:

;

;

.

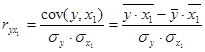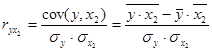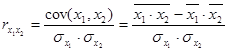Standardized β-coefficients (2.5):

;

.

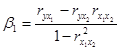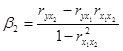So, the equation of regression in standardized form has a view of: .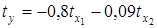

Conclusion: Comparison of absolute values of standardized coefficients of regression (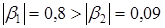) says that age (x1) of automobile influences too much to the price than the mileage(х ₂).

Calculate the natural regression coefficients:

;

;

.

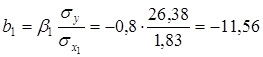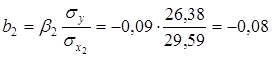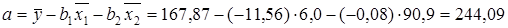An equation linear multiple (two-factor) in the natural form of the regression: .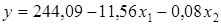

Conclusion: With increasing age of the car for 1 year its price has decreased by an average of 11,56 th.tg, and with the increase in mileage per 1 thousand km price is reduced by an average of 0,08 tg (80tg).

2. Найдем коэффициенты множественной и частной корреляции, а также множественной детерминации.

Коэффициент множественной корреляции находится по формуле:

.

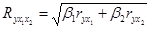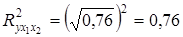– коэффициент множественной детерминации.

Вывод: величина коэффициента множественной корреляции показывает, что связь между y, x ₁, x ₂ – высокая[1], причем 76,3% вариации цены на автомобиль объясняется вариацией возраста машины и пробега.

Коэффициенты частной корреляции определяются через парные коэффициенты корреляции по формулам:

;

;

.

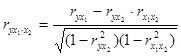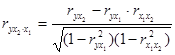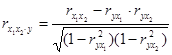Вывод: коэффициенты частной корреляции характеризуют тесноту связи между двумя переменными, исключив влияние третьей переменной. Значит, связь между ценой на ВАЗ 2110 и годом выпуска при исключении влияния величины пробега обратная и заметная; между ценой автомобиля и пробегом без учета возраста машины – обратная, но слабая; связь между факторами x ₁ и x ₂ – умеренная.

Сравним соответствующие коэффициенты парной и частной корреляции: , , ;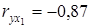

, , .

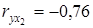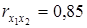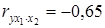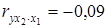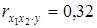Вывод:

1) при закреплении фактора x ₂ на постоянном уровне влияние на y фактора x ₁ оказалось несколько менее сильным (– 0,65 против – 0,87), но все равно остается заметным;

2) при закреплении фактора x ₁ на постоянном уровне влияние на y фактора x ₂ стало весьма слабым (– 0,09 против – 0,76);

3) межфакторная связь (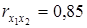) говорит о высокой коллинеарности факторов, причем исключив влияние результативной переменной y эта связь становится умеренной.

3. Оценим значимость уравнения регрессии и коэффициента множественной детерминации с помощью F-критерия Фишера. Наблюдаемое значение критерия находится по формуле:

.

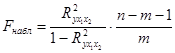Табличное значение критерия при уровне значимости a = 0,05 и , :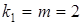

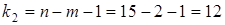F_табл = F (0,05; 2; 12) = 3,88.

Вывод: т.к. F_табл < F_набл, то с вероятностью 1 – a = 0,95 делаем заключение о статистической значимости уравнения регрессии и коэффициента множественной детерминации, которые сформировались под неслучайным воздействием факторов 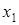и .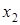

Оценим целесообразность включения в уравнение множественной регрессии фактора х ₁ после фактора х ₂ и целесообразность включения фактора х ₂ после фактора х ₁ с помощью частных F-критериев 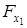и .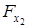

;

.

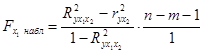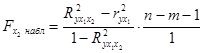Найдем табличные значения критерия на уровне значимости a = 0,05 и 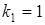, 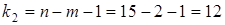: F_табл = F (0,05; 1; 12) = 4,75.

Вывод: 1) Поскольку 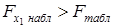, то включение в модель фактора х ₁ (возраста автомобиля) после фактора х ₂ статистически оправдано и коэффициент b ₁ при факторе х ₁ статистически значим.

2) Поскольку 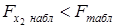, то нецелесообразно включать в модель фактор х ₂ (пробег) после фактора х ₁. Это означает, что парная регрессия зависимости цены ВАЗ 2110 от возраста машины является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор х ₂.

Найдем уравнение парной регрессии 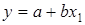, где y – цена автомобиля (тыс. руб), х ₁ – возраст машины (лет):

;

.

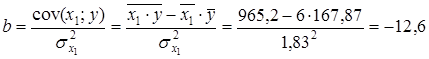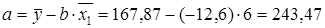Получаем: .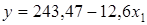

Coefficient of elasticity

Coefficient of elasticity is the indicator of influence to the factor.

Э̄_yx=f(x₁)(x̄₁/ȳ)

1) Э̄_yx=(b*x̄)/(a+b*x̄) – linear method

2) 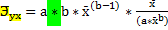= b - degreed function

3) 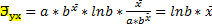-exponential method

Compare the results of elasticity.

[1] При качественной интерпретации коэффициента корреляции используется шкала Чеддока

Дата добавления: 2015-08-17