Контроль достовірності рішення

Для того, щоб розв’язок задачі лінійного програмування вважався достовірним, повинні виконуватися 3 умови:

припустимість;

опірність;

оптимальність.

При невиконанні хоча б однієї з умов достовірності, розв’язок не вважається достовірним.

Перевіримо припустимість отриманого розв’язку задачі лінійного програмування. Для цього помножимо кожен елемент матриці умов на знайдене значення x* та просумуємо. Результат повинен дорівнювати вектору обмежень з точністю ε = 10^-6.

,

де - розрахований вектор обмежень, - заданий вектор обмежень.

X^* =

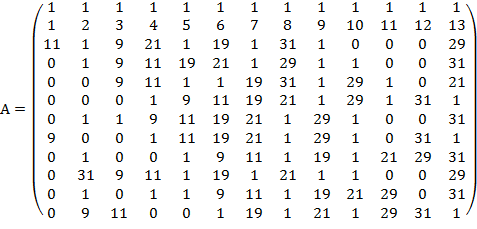
Робимо множення матриці А на вектор Х^*:

b`₁=(1)*(3.3273)+(1)*(3.21436)+(1)*(35.34397)+(1)*(7.77647)+(1)*(1.91608)+(1)*(19.44581)+(1)*(2.04495)+(1)*(0)+(1)*(11.1295)+(1)*(17.93412)+(1)*(2.90471)+(1)*(13.43781)+(1)*(11.52493) = 130.000001

b`<sub>2</sub>=(1)*(3.3273)+(2)*(3.21436)+(3)*(35.34397)+(4)*(7.77647)+(5)*(1.91608)+(6)*(19.44581)+(7)*(2.04495)+(8)*(0)+(9)*(11.1295)+(10)*(17.93412)+(11)*(2.90471)+(12)*(13.43781)+(13)*(11.52493)=910.0000004 b`₃=(11)*(3.3273)+(1)*(3.21436)+(9)*(35.34397)+(21)*(7.77647)+(1)*(1.91608)+(19)*(19.44581)+(1)*(2.04495)+(31)*(0)+(1)*(11.1295)+(0)*(17.93412)+(0)*(2.90471)+(0)*(13.43781)+(29)*(11.52493)=1240.000001 b`<sub>4</sub>=(0)*(3.3273)+(1)*(3.21436)+(9)*(35.34397)+(11)*(7.77647)+(19)*(1.91608)+(21)*(19.44581)+(1)*(2.04495)+(29)*(0)+(1)*(11.1295)+(1)*(17.93412)+(0)*(2.90471)+(0)*(13.43781)+(31)*(11.52493)=1240.00000019 b`₅=(0)*(3.3273)+(0)*(3.21436)+(9)*(35.34397)+(11)*(7.77647)+(1)*(1.91608)+(1)*(19.44581)+(19)*(2.04495)+(31)*(0)+(1)*(11.1295)+(29)*(17.93412)+(1)*2.90471)+(0)*(13.43781)+(21)*(11.52493)=1240.0000006 b`<sub>6</sub>=(0)*(3.3273)+(0)*(3.21436)+(0)*(35.34397)+(1)*(7.77647)+(9)*(1.91608)+(11)*(19.44581)+(19)*(2.04495)+(21)*(0)+(1)*(11.1295)+(29)*(17.93412)+(1)*(2.90471)+(31)*(13.43781)+(1)*(11.52493)=1239.999999 b`₇=(0)*(3.3273)+(1)*(3.21436)+(1)*(35.34397)+(9)*(7.77647)+(11)*(1.91608)+(19)*(19.44581)+(21)*(2.04495)+(1)*(0)+(29)*(11.1295)+(1)*(17.93412)+(0)*(2.90471)+(0)*(13.43781)+(31)*(11.52493)=1240.00000023 b`<sub>8</sub>=(9)*(3.3273)+(0)*(3.21436)+(0)*(35.34397)+(1)*(7.77647)+(11)*(1.91608)+(19)*(19.44581)+(21)*(2.04495)+(1)*(0)+(29)*(11.1295)+(1)*(17.93412)+(0)*(2.90471)+(31)*(13.43781)+(1)*(11.52493)=1240.0000005 b`₉=(0)*(3.3273)+(1)*(3.21436)+(0)*(35.34397)+(0)*(7.77647)+(1)*(1.91608)+(9)*(19.44581)+(11)*(2.04495)+(1)*(0)+(19)*(11.1295)+(1)*(17.93412)+(21)*(2.90471)+(29)*(13.43781)+(31)*(11.52493)=1240.0000003 b`<sub>10</sub>=(0)*(3.3273)+(31)*(3.21436)+(9)*(35.34397)+(11)*(7.77647)+(1)*(1.91608)+(19)*(19.44581)+(1)*(2.04495)+(21)*(0)+(1)*(11.1295)+(1)*(17.93412)+(0)*(2.90471)+(0)*(13.43781)+(29)*(11.52493)=1240.0000007 b`₁₁=(0)*(3.3273)+(1)*(3.21436)+(0)*(35.34397)+(1)*(7.77647)+(1)*(1.91608)+(9)*(19.44581)+(11)*(2.04495)+(1)*(0)+(19)*(11.1295)+(21)*(17.93412)+(29)*(2.90471)+(0)*(13.43781)+(31)*(11.52493)=1240.000001 b`₁₂=(0)*(3.3273)+(9)*(3.21436)+(11)*(35.34397)+(0)*(7.77647)+(0)*(1.91608)+(1)*(19.44581)+(19)*(2.04495)+(1)*(0)+(21)*(11.1295)+(1)*(17.93412)+(29)*(2.90471)+(31)*(13.43781)+(1)*(11.52493) = 1240.0000002

|130 – 130.000001| = 0.000001 ≤ ε

|910 – 910.0000004 | = 0.0000004≤ ε

|1240 – 1240.000001 | = 0.000001 ≤ ε

|1240 – 1240.00000019 | = 0.00000019 ≤ ε

|1240 – 1240.0000006 | = 0. 0000006 ≤ ε

|1240 – 1239.999999 | = 0.000001 ≤ ε

|1240 – 1240.00000023 | = 0.00000023 ≤ ε

|1240 – 1240.0000005 | = 0.0000005 ≤ ε

|1240 – 1240.0000003 | = 0. 0000003 ≤ ε

|1240 – 1240.0000007 | = 0. 0000007 ≤ ε

|1240 – 1240.000001 | = 0.000001 ≤ ε

|1240 – 1240.0000002| = 0.0000002 ≤ ε

Отже, розв’язок є припустимим.

Перевіримо опірність отриманого розв’язку. Для цього зробимо перевірку лінійної незалежності векторів 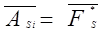шляхом розрахунку детермінанту матриці 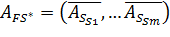. Якщо , то вектори умов, відповідні базисним компонентам лінійно-незалежні та задають вершину припустимої множини задачі лінійного програмування.

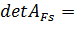= 2.72653*e¹⁷ = 65859203.32 > ε

Рисунок 2.20 – Розрахунок детермінанту матриці засобами Excel

Отже, розв’язок є опірним.

Перевіримо оптимальність знайденого розв’язку. Для цього підставляємо знайдені значення та 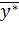у формули , , Якщо , то вважається справедливим виконання рівності та робиться висновок про достовірність розв’язків та 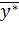задач двоїстої пари, отриманих за допомогою розробленої програми.

L = 484 x₁ + 907 x₂ + 1612 x₃ + 2599 x₄ + 3868 x₅ + 5419 x₆ + 7252 x₇ +9367 x₈ +11764 x₉ +14443 x₁₀ + 17404 x₁₁ + 20647 x₁₂ + 24172 x₁₃ → max

x* = (3.3273; 3.21436; 35.34397; 7.77647; 1.91608; 19.44581; 2.04495; 0; 11.1295; 17.93412; 2.90471; 13.43781; 11.52493)

L* = 484 3.3273 + 907 3.21436 + 1612 35.34397 + 2599 7.77647 + 3868 1.91608 + 5419 19.44581 + 7252 2.04495 + 9367 0 + 11764 11.1295 + 14443 17.93412 + 17404 2.90471 + 20647 13.43781 + 24172 11.52493 = 1205864.13879566

= 130 y₁ + 910 y₂ + 1240 y₃ + 1240 y₄ + 1240 y₅ + 1240 y₆ + 1240 y­₇ + 1240 y₈ + 1240 y₉ + 1240 y₁₀ + 1240 y₁₁ + 1240 y₁₂ → min

y* = (-902.2697; 1508.191; -116.0761; -15.5243; 193.1788; -177.3166; -254.9067; 128.3239; 420.2969; 27.99196; -12.85522; -232.8664)

130 (-902.2697) + 910 (1508.191) + 1240 (-116.0761) + 1240 (-15.5243) + 1240 (193.1788) + 1240 (-177.3166) + 1240 (-254.9067) + 1240 (128.3239) + 1240 (420.2969) + 1240 (27.99196) + 1240 (-12.85522) + 1240 (-232.8664) = 1205864.13879615

Отже = .

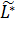Знайдене рішення оптимальне.

Усі вищевказані результати були отримані в процесі ручного розрахунку. Нижче наведено варіант перевірки достовірності рішення і всіх вищевказаних пунктів за допомогою розробленого програмного забезпечення

Рисунок 2.21 – Результат роботи розробленого ПЗ в мідменю «Достоверность»

Дата добавления: 2015-08-17