Периодические функции и их свойства.

Гл. Ряды Фурье. Интеграл Фурье.

Пусть f(x) функция определена а всей числовой оси

Df1. Число Т называется периодом f(x) если для ∀ x ∈ R справедливо равенство

f(x+T) =f(x), T>0

Df2. Функция имеющая период отличный от нуля называется периодической.

Основные свойства периодических функций

1. Если Т – период функции, то 2Т; 3Т,… и т.д. nT где n∈ также будет периодом

2. Если функция f(x) имеет период Т, то функция f(ax) имеет периодом число ;

f [a(x+ )]= f (ax+Т)= f(ax).

3. Если f(x) ϵC[R] имеет период Т, то интеграл этой функции взятый в пределах отличающийся на Т, не зависит от выбора нижнего предела интегрирования, т.е.

Cϵ

Доказательство:

	y

2 T

3 T /2

T

T /2

x

S₂^*

S₁^*

S₁

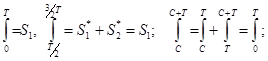
4. Сумма, разность, произведение и частное периодических функций периода Т, есть периодические функции того же периода.

Дата добавления: 2015-08-17