Решение. 1. Используя разложение:

1. Используя разложение:

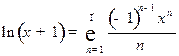, , получим:

.

Отсюда находим:

.

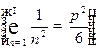2. Преобразуем подынтегральную функцию

и в исходном интеграле сделаем замену переменной:

.

Раскладывая теперь в ряд Маклорена функцию:

,

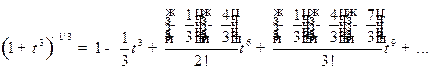получим:

Если сохранить только два члена, то погрешность не будет превышать .

Таким образом:

, .

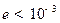3. Запишем ряд Маклорена для функции :

, .

Для это равенство примет вид:

,

.

4. Будем искать решение уравнения в виде степенного ряда:

.

Тогда

,

.

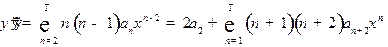Уравнение примет вид:

.

Приравнивая коэффициенты при одинаковых степенях , получим:

, , .

Так как , то согласно рекуррентному соотношению:

, ,..., .

Из этого же соотношения:

,

.

Поскольку

,

то решение уравнения 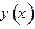принимает вид:

Дата добавления: 2015-08-17