Решение. 1. Представим рациональную функцию в виде суммы элементарных рациональных дробей:

1. Представим рациональную функцию в виде суммы элементарных рациональных дробей:

.

Используя разложения (10) и (11), получим:

, ;

, .

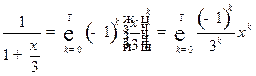Окончательно:

,

где .

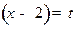2. В этом случае нужно разложить функцию в окрестности точки , то есть по степенями . Полагая , получим:

.

Используя формулы (13) и (14), находим:

, .

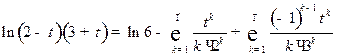Отсюда окончательно получим:

, .

3. Поскольку :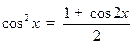

.

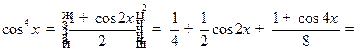
Обозначим , , тогда:

,

.

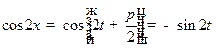И поэтому:

.

Используя формулы (5) и (6), получим:

, .

4. Вычислим производную заданной функции ,

.

Из разложения (12) следует, что

, .

Интегрируя полученный ряд почленно, получаем:

, ,

.

Окончательно имеем:

, .

6°. Ряды Тейлора часто используют для вычисления сумм числовых рядов, интегралов, вычисления приближенных значений функций, интегралов, решения дифференциальных уравнений.

Дата добавления: 2015-08-17