
Читайте также:
|
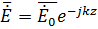 волна ТЕМ.
волна ТЕМ.
Пусть волна распространяется вдоль оси z. Вектор 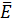 имеет
имеет  если
если 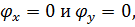 то
то 
Рис. 2.7
 – составляет с осью oz угол
– составляет с осью oz угол 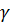 .
.
Тогда вектор  можно разложить на
можно разложить на 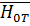 и
и 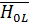 .
.
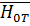 – поперечная составляющая,
– поперечная составляющая, 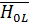 – продольная составляющая.
– продольная составляющая.
То есть 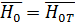 +
+ 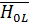 ,
, 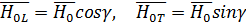 .
.
Вектор 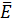 можно разложить на
можно разложить на 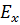 и
и 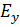 .
.
Для упрощения выкладок (не теряя общности) повернем оси xy так вокруг оси oz, чтобы направление 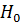 совпало с направлением одной из осей ox или oy.
совпало с направлением одной из осей ox или oy.
Мы примем, что 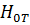 совпадает с осью oy, то есть
совпадает с осью oy, то есть 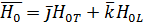 . (можно рассмотреть и общий случай, когда волна имеет все компоненты Ех, Еу, Ez).
. (можно рассмотреть и общий случай, когда волна имеет все компоненты Ех, Еу, Ez).
При решении задачи будем исходить:
1) из уравнения движения электрона в электромагнитном поле при наличии постоянно магнитного поля Земли  :
:
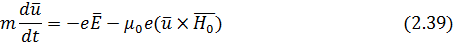
(действием магнитного поля волны на электрон пренебрегаем, так как оно мало по сравнению с 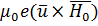 ).
).
2) из уравнений электромагнитного поля (уравнений Максвелла) имеем:
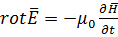
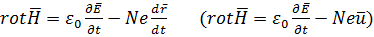 .
.
Поскольку колебания гармонические, то перейдем к комплексным амплитудам, тогда можно записать
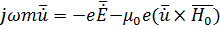 ,
, 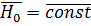 магнитное поле Земли
магнитное поле Земли 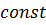 .
.
или

Уравнения электромагнитного поля будут иметь вид:
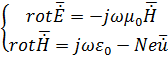
Исключим 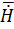 , получим уже одно уравнение (для этого возьмем
, получим уже одно уравнение (для этого возьмем  от 1-го уравнения и подставим
от 1-го уравнения и подставим 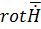 ):
):
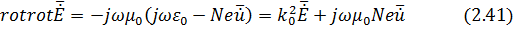
Для совместного решения уравнений (2.40) и (2.41) разложим их на скалярные уравнения, то есть:
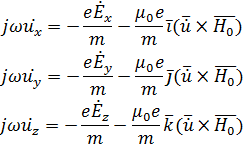
Найдем 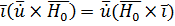 – (на основании свойства смешанного произведения векторов).
– (на основании свойства смешанного произведения векторов).
Так как 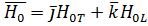 , то
, то 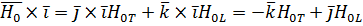
Отсюда 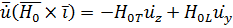 (на основании правила скалярного умножения двух векторов или
(на основании правила скалярного умножения двух векторов или  ):
):
 ;
;
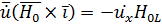 .
.
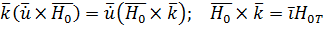 ;
;
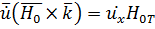 .
.
Если обозначить:
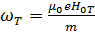 – поперечная гиромагнитная частота.
– поперечная гиромагнитная частота.
 – продольная гиромагнитная частота.
– продольная гиромагнитная частота.
То получим:
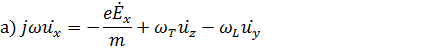

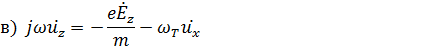
Из уравнения в) видно, что электрон приобретает скорости не только вдоль осей х и у, то есть поперечные скорости, но и продольную скорость 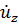 (так как имеется две составляющие магнитного поля). Как будет видно далее эта составляющая скорости
(так как имеется две составляющие магнитного поля). Как будет видно далее эта составляющая скорости 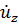 приводит к появлению продольной составляющей электрического поля
приводит к появлению продольной составляющей электрического поля 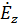 , хотя она в первоначальном поле отсутствовала.
, хотя она в первоначальном поле отсутствовала.
Разложим теперь уравнение электромагнитного поля (2.41) на скалярные.
Найдем вначале  :
:
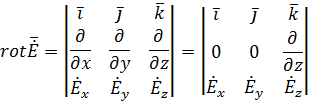
Так как волна распределяется вдоль оси oz и она является плоской, однородной, то от координат х и у она не зависит, следовательно
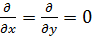 .
.
Так как 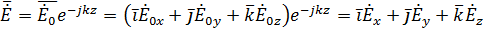
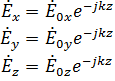
Где k – волновой множитель, пока еще неизвестный, который мы еще ищем.
Следовательно 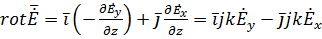 – здесь имеются только две составляющие по х и у.
– здесь имеются только две составляющие по х и у.
Найдем  :
:
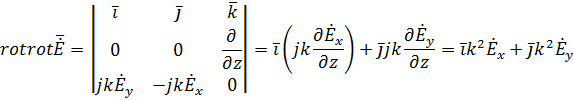
Следовательно получим:
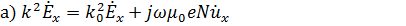


Из уравнений 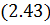 видно, что наличие
видно, что наличие 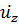 приводит к появлению
приводит к появлению  (если положить
(если положить 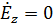 , то и
, то и 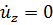 , но тогда не удовлетворяется условие уравнение
, но тогда не удовлетворяется условие уравнение 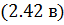 ).
).
Таким образом мы получим две системы 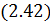 и
и 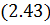 , содержащие
, содержащие 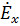 ,
, 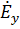 ,
, 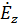 ,
, 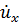 ,
, 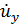 ,
, 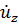 и неизвестную величину k.
и неизвестную величину k.
В нашу задачу входит определение величины k или то же самое величины  - относительная диэлектрическая проницаемость.
- относительная диэлектрическая проницаемость.
Так как 
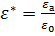 ,
,  .
.
Данные системы 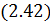 и
и 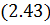 совместных однородных уравнений могут иметь решения, отличные от 0 только в том случае, если определитель состоящий из коэффициентов при неизвестных равен 0.
совместных однородных уравнений могут иметь решения, отличные от 0 только в том случае, если определитель состоящий из коэффициентов при неизвестных равен 0.
Если приравниваем определитель 0, то получим  или
или 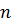 или
или  (то есть мы ищем такое
(то есть мы ищем такое  , когда определитель будет равен 0):
, когда определитель будет равен 0):
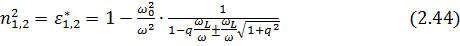
- значение диэлектрической проницаемости  .
.
Здесь 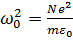 – собственная частота ионизированного газа, или частота Ленгмюра, или плазменная частота, в радиотехнике – критическая частота:
– собственная частота ионизированного газа, или частота Ленгмюра, или плазменная частота, в радиотехнике – критическая частота:

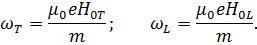
Из выражения (2.44) видно, что получили 2 решения, то есть два значения диэлектрической проницаемости – это характеризуется знаками 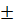 в знаменателе, (два значения коэффициента преломления), то есть имеет место двойное лучепреломление. Имеются как бы два луча (две волны), имеющих свои фазовые скорости, свои показатели преломления, то есть волна при прохождении через ионосферу в постоянном магнитном поле в общем случае расщепляется на две волны (в оптике кристалл турмалина).
в знаменателе, (два значения коэффициента преломления), то есть имеет место двойное лучепреломление. Имеются как бы два луча (две волны), имеющих свои фазовые скорости, свои показатели преломления, то есть волна при прохождении через ионосферу в постоянном магнитном поле в общем случае расщепляется на две волны (в оптике кристалл турмалина).
1) Волна, с диэлектрической проницаемостью (показатель преломления), содержащей + перед корнем называется обыкновенной 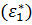 .
.
2) Волна, с диэлектрической проницаемостью (показатель преломления), содержащей – перед корнем называется необыкновенной 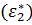 .
.
Если используем системы 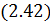 и
и 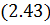 , то можно получить для каждой волны соотношения между поперечными компонентами электрического поля:
, то можно получить для каждой волны соотношения между поперечными компонентами электрического поля:

Знаки 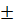 составляют обыкновенным и необыкновенным волнам соответственно.
составляют обыкновенным и необыкновенным волнам соответственно.
Из (2.46) следует, что как для обыкновенных так и необыкновенных волн между компонентами 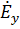 и
и 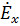 имеется сдвиг по фазе на
имеется сдвиг по фазе на  , а поскольку компоненты поля в общем случае не равны между собой (они равны только при
, а поскольку компоненты поля в общем случае не равны между собой (они равны только при 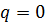 ), то волны оказываются эллиптически поляризованными.
), то волны оказываются эллиптически поляризованными.
Причем поскольку 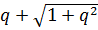 и
и 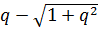 имеют противоположные знаки, так как
имеют противоположные знаки, так как  , то вращение вектора (направление вращения) для обыкновенных и необыкновенных волн противоположны.
, то вращение вектора (направление вращения) для обыкновенных и необыкновенных волн противоположны.
(Обыкновенные – против часовой стрелки, необыкновенные – по часовой стрелки по отношению к магнитному полю 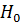 ).
).
(При 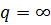 - линейная поляризация).
- линейная поляризация).
Все сказанное справедливо для проекции вектора 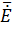 на плоскость перпендикулярную направлению распространения волны.
на плоскость перпендикулярную направлению распространения волны.
Если учесть, что 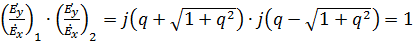 , то получим
, то получим 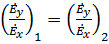 . Получили уравнение эллипса (1 – обыкновенная волна, 2 – необыкновенная волна).
. Получили уравнение эллипса (1 – обыкновенная волна, 2 – необыкновенная волна).
Так как фаза между 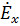 и
и 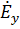 равна
равна  , то эллипс будет вытянут либо вдоль оси х, либо вдоль оси у.
, то эллипс будет вытянут либо вдоль оси х, либо вдоль оси у.
Необходимо помнить, что имеется еще продольная составляющая 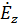 , который вносит свой вклад в электромагнитное поле и его поляризацию.
, который вносит свой вклад в электромагнитное поле и его поляризацию.
Если учтем столкновения электронов, то это приведет к появлению коэффициента затухания – различного для различных волн.
Коэффициент затухания у необыкновенной волны больше чем у обыкновенной.
Напряженность поля 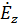 волны находится в следующем соотношении с
волны находится в следующем соотношении с 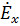 и
и 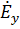 :
:
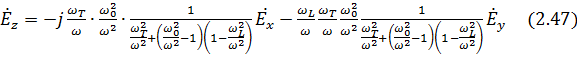
Получим уже волну  - волну (вместо ТЕМ).
- волну (вместо ТЕМ).
Отсюда видно, что 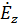 находится в фазе с
находится в фазе с 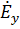 и сдвинута по фазе на угол
и сдвинута по фазе на угол 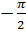 по отношению к
по отношению к 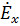 .
.
Следовательно, в общем случае вектор 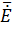 описывает эллипс в плоскости параллельной оси х.
описывает эллипс в плоскости параллельной оси х.
Учитывая, что 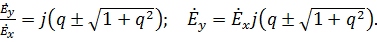
Если выразим 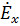 через
через 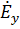 и подставим в (2.47), то получим
и подставим в (2.47), то получим 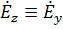 (пропорциональны), то есть они колеблются в фазе.
(пропорциональны), то есть они колеблются в фазе.
Отсюда следует, что вектор 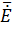 в общем случае описывает эллипс в плоскости параллельной оси ох.
в общем случае описывает эллипс в плоскости параллельной оси ох.
Рис. 2.8
После получения основных соотношений перейдем к рассмотрению двух крайних случаев:
1) продольного магнитного поля.
2) поперечного магнитного поля.
Рассмотрение этих случаев играет важную роль, как будет показано ниже, во всех практически важных случаях приближенно можно перейти к этим случаям.
Дата добавления: 2015-08-17; просмотров: 108 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Гиромагнитный резонанс. | | | Распространение радиоволн в направлении постоянного магнитного поля Земли. |