Оценка полученных результатов

При заданных установках режим «Регрессия» рассчитает три таблицы: «Регрессионная статистика», «Дисперсионный анализ», «Коэффициенты и оценки». Из-за ограниченности объема статьи рассмотрим не все значения в таблицах. Логичнее начать со второй таблицы.

Таблица «Дисперсионный анализ»

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		13119,56	13119,56	57,09	0,0016
Остаток		919,27	229,82
Итого		14038,83

Столбец df содержит число степеней свободы k, знаменатели при вычислении несмещенных выборочных дисперсий MS=SS/k. Для регрессии это число регрессоров k_рег=m= 1. Для остатка это k_ост=N−(m+ 1 ), число исходных точек минус число коэффициентов уравнения регрессии и минус свободный член. Для выборочной общей дисперсии, строка «Итого», число степеней свободы k_общ=N− 1. Одна степень свободы «украдена» свободным членом регрессионного уравнения.

Степени свободы связаны соотношением: k_общ = k_рег + k_ост

Столбец SS содержит суммы квадратов отклонений от среднего значения результирующего признака .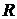

Регрессия регрессионная или факторная, сумма квадратов уклонений от 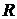теоретических значений, рассчитанных по регрессионному уравнению.

Остаток остаточная, сумма квадратов уклонений исходных значений от теоретических значений.

Итого 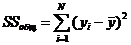общая, сумма квадратов уклонений исходных значений от 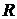. Она записана в строке «».

Суммы связаны основным соотношением дисперсионного анализа:

SS_общ = SS_рег + SS_ост

Чем больше SS_рег (или чем меньше SS_ост), тем лучше регрессионное уравнение аппроксимирует облако исходных точек. В нашем случае SS_ост мала по сравнению с SS_общ. Уравнение регрессии хорошо аппроксимирует облако исходных точек.

Столбец MS содержит несмещенные выборочные дисперсии, регрессионную и остаточную, степеней свободы взяты из столбца df.

MS_рег = SS_рег / m MS_ост = SS_ост / (N – m –1 )

Таблица «Регрессионная статистика»

Регрессионная статистика
Множественный R	0,9667
R–квадрат	0,9345
Нормированный R–квадрат	0,9181
Стандартная ошибка	15,1598
Наблюдения

R–квадрат для характеристики качества регрессионного уравнения вычисляется безразмерная величина, коэффициент детерминации R ², или квадрат коэффициента множественной корреляции (Множественный R)

R² = SS_рег / SS_общ = 0,9345

То есть 93,45% вариации результирующего признака Y объясняется вариацией регрессоров X1 и X2. Другими словами, 93,45% изменений признака Y описывается регрессионным уравнением, а 6,55% – другими причинами.

Нормированный R–квадрат скорректированный (адаптированный, подправленный – adjusted) коэффициент детерминации:

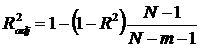
Недостатком коэффициента детерминации R ² является то, что он увеличивается при добавлении новых регрессоров, потому что при этом всегда увеличивается сумма SS_рег. Но это не обязательно означает улучшение качества регрессионной модели. Коэффициент нового регрессора может оказаться незначимым, слишком широк его доверительный интервал..

В этом смысле предпочтительнее использовать 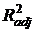. Добавление нового регрессора увеличивает SS_рег, R ², уменьшает числитель и знаменатель (m увеличивается на 1). Формула устроена так, что 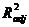увеличится, если только достаточно значимо возрастет сумма SS_рег.

При добавлении или исключении из уравнения очередного регрессора нужно сравнивать 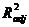с предыдущим значением.

Стандартная ошибка содержит несмещенное выборочное остаточное стандартное отклонение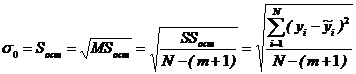

Обратите внимание, что нельзя вычислить выборочное остаточное стандартное отклонение, когда число исходных точек равно числу коэффициентов уравнения регрессии, или меньше.

Так же как и коэффициент 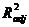, параметр σ ₀ нужно сравнивать с предыдущим расчетом для другого числа регрессоров.

Таблица «Коэффициенты и оценки»

Коэффициенты и оценки	Коэффи циенты	Стандартная ошибка	t-стати стика	P-Зна чение	Нижние 95%	Верхние 95%
Y–пересечение	-23,0425	20,0648	-1,1484	0,3148	-78,7514	32,6664
X1	1,7375	0,2300	7,5556	0,0016	1,0990	2,3759

Последняя таблица содержит коэффициенты для регрессоров и их оценки. Названия строк показывают, с каким регрессором связаны рассчитанные значения. Строка Y-пересечение не связана ни с одним регрессором, это свободный коэффициент.

Столбец Коэффициенты содержит значения коэффициентов уравнения регрессии. Здесь получилось: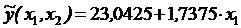

Регрессионное уравнение должно проходить через центр облака исходных точек. Если подставить в регрессионное уравнение средние значения по регрессору X1=83,000, то должно получиться среднее значение по зависимому признаку Y=121,167. Все правильно.

Большинство пользователей смотрит только этот столбец и, не задумываясь, использует уравнение регрессии в своих исследованиях. Но вычисление коэффициентов уравнения регрессии это обычная оптимизационная задача построения аппроксимирующего уравнения.

Математическая статистика начинается с анализа стандартных ошибок коэффициентов и расчета интервальных оценок регрессионного уравнения. Это может в корне перевернуть выводы, сделанные неискушенным исследователем. Оптимист – это плохо информированный пессимист.

Столбец Стандартная ошибка содержит выборочные стандартные отклонения по каждому коэффициенту уравнения регрессии, стандартные ошибки коэффициентов. Они вычисляются по формулам:

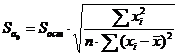
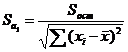
Если стандартная ошибка больше абсолютной величины коэффициента, это коэффициент незначимый. Этот коэффициент (свободный член или регрессор) нужно исключить из уравнения регрессии и пересчитать таблицы. Но это грубый анализ. Столбец t-статистика дает более точную оценку значимости коэффициентов.

Общая причина большой стандартной ошибки – большое значение остаточной суммы квадратов уклонений SS_ост, малое число исходных точек N и малое значение дисперсии по X. Для отдельных регрессоров это может быть компенсировано большой дисперсией по X (она в знаменателе стандартной ошибки). Регрессоры с малыми единицами измерения – первые кандидаты на удаление. Положение может поправить нормализация исходных данных.

Столбец t-статистика содержит значения t -критерия, рассчитанные по формуле: t_р = (Коэффициент) / (Стандартная ошибка)

Этот критерий имеет закон распределения Стьюдента с числом степеней свободы N− (m+ 1): число исходных точек, минус число регрессоров, минус свободный член, если есть.

Если коэффициент a_i значимый для регрессионного уравнения, должна быть отвергнута гипотеза H ₀: a_i =0 – регрессор не входит в уравнение. Для этого при стандартном уровне надежности 95% соответствующий критерий t_i должен попадать в 5% двухстороннюю критическую область. Для нашего случая вычислим границу критической области ± t_кр:

t_кр = СТЬЮДРАСПОБР(1–0,95; 6–1–1) = 2,78

Незначимым оказался свободный член: 1,1484 < 2,78. Чтобы исключить его из регрессионного уравнения, нужно в окне «Регрессия» установить флажок Константа-ноль и снова выполнить макрос.

Столбцы Нижние 95% и Нижние 95% содержат границы 95%-го доверительного интервала, для каждого коэффициента – свои границы:

Коэффициент ± t_кр × Стандартная ошибка

Стандартная ошибка у каждого коэффициента своя, t_кр =2,78 – общее, его уже вычисляли для t-статистики.

Как понимать границы 95%-го доверительного интервала. Если бы мы обрабатывали 100 групп по 6 предприятий, по каждой группе получилась бы своя пара коэффициентов регрессионного уравнения. Но 95 пар коэффициентов из 100 будут находиться внутри 95%-х интервалов.

Интервальные оценки коэффициентов регрессионного уравнения
y= β ₀ + β ₁· x имеют вид:

Тогда интервальная оценка регрессионного уравнения в текущей точке x ₀

Обратите внимание. Из этой формулы следует, минимальная ширина доверительного интервала в центре облака исходных точек, когда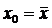

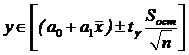
Рассчитаем интервальные оценки регрессионного уравнения в 6 исходных точках, а также в дополнительных точках 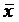, , 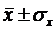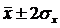. Получим таблицу интервальных оценок. Здесь дополнительные точки выделены курсивом.

	X	Радиус	Y	Yрег	Y-	Y+	Отношение
Xср−2 σ	24,036	41,383		19	-23	60	0,5809
		28,698					0,4029
Xср− σ	53,518	25,487		70	44	95	0,3578
		21,034					0,2953
		19,369					0,2719
Xср	83,000	17,183		121	104	138	0,2412
		17,372					0,2439
		21,034					0,2953
Xср+ σ	112,482	25,487		172	147	198	0,3578
		34,027					0,4777
Xср+2 σ	141,964	41,383		224	182	265	0,5809

В последнем столбце рассчитано отношение ширины доверительного 95%-го интервала (Y+)–(Y-) к размаху по Y регрессионного уравнения: 201 (макс) – 59 (мин) = 142.

В Excel построим на диаграмме облако исходных точек, регрессионное уравнение, верхнюю и нижнюю границу доверительного интервала.

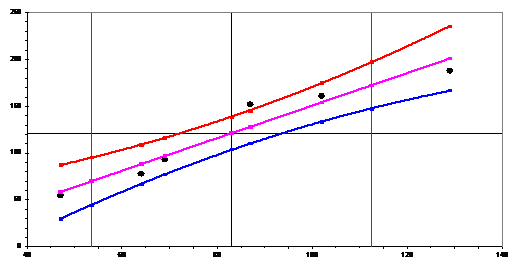
Здесь вертикальными линиям отмечены точки .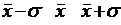

Выводы. Даже в центре облака относительная ширина 95%-го доверительного интервала составляет 24%; в точках ± σ – 36%, или в 1,5 раза шире, чем в центре; в точках ±2 σ – 58%, или в 2,4 раза шире, чем в центре. Точки ±2 σ находятся за пределами облака исходных точек и обычно используются для расчета прогнозных значений по регрессионному уравнению. Такова точность экономических прогнозов.

Дата добавления: 2015-08-17