
Читайте также:
|
Раздел «Аналитическая геометрия»
1) Найдите точку пересечения прямой и плоскости
a) 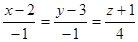 ; y+2y+3z–14=0
; y+2y+3z–14=0
b) 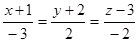 ; x+3y–5z+9=0
; x+3y–5z+9=0
c) 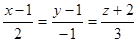 ; 4x+2y–z–11=0
; 4x+2y–z–11=0
2) Определить тип кривой и построить эту кривую в системе координат OXY
a) 25 x2 + 169 y2 = 4225
b) 576 x2 – 49 y2 = 28224
c) x2 = –8x – 12y – 4
Раздел «Алгебра и геометрия»
1) Разложить многочлен 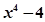 на неприводимые над R и C.
на неприводимые над R и C.
[Ответ: 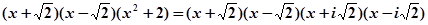 ]
]
2) Даны векторы 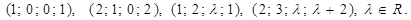
При каких  указанные векторы образуют базис пространства
указанные векторы образуют базис пространства 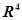 ?
?
[Ответ: при 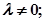 ]
]
3) Линейный оператор в 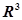 задан матрицей
задан матрицей 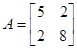 . Диагонализировать его (найти ортонормированный базис из собственных векторов).
. Диагонализировать его (найти ортонормированный базис из собственных векторов).
[Ответ: 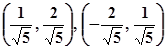 ]
]
Раздел «Дискретная математика»
1) Получить известную формулу для суммы 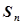 первых
первых  членов геометрической прогрессии, составив и решив рекуррентное уравнение для последовательности
членов геометрической прогрессии, составив и решив рекуррентное уравнение для последовательности 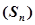
2) Для графа G найти циклический ранг и какой-нибудь остов, эйлерову цепь, плоский граф, изоморфный графу G, где:
а) G – куб;
в) G – октаэдр.
Раздел «Математический анализ»
1. Вычислите пределы: а) 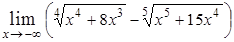 ; б)
; б) 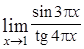 ; в)
; в) 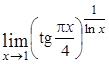 ; г)
; г) 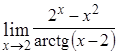 ; д)
; д) 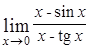 .
.
2. Найти суммы рядов: а) 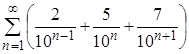 ; б)
; б) 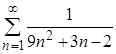 .
.
3. Найти интегралы: а) 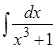 ; б)
; б) 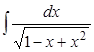 ; в)
; в) 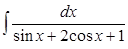 ; г)
; г) 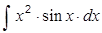 ; д)
; д) 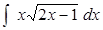 .
.
4. Вычислить площади фигур, ограниченных линиями: а) 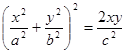 ; б)
; б) 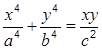 .
.
5. Вычислить криволинейный интеграл 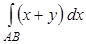 , если
, если 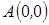 ,
,  и а)
и а) 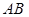 - отрезок прямой; б)
- отрезок прямой; б) 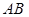 - дуга параболы
- дуга параболы 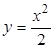 ; в)
; в)  - ломаная
- ломаная  , где
, где 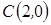 .
.
6. Вычислить криволинейный интеграл 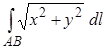 , где
, где 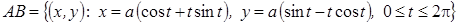 .
.
7. Исследовать на экстремум: 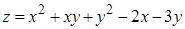 ;
; 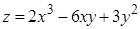 .
.
8. Исследовать на условный экстремум: а) 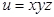 ,
, 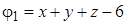 ;
; 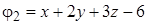 . б)
. б) 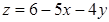 ,
, 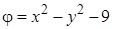 .
.
9. Найдите интервал и радиус сходимости, исследуйте на абсолютную или условную сходимость на границах интервала: а) 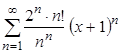 ; б)
; б) 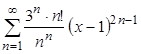 ; г)
; г) 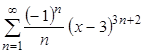 .
.
10. Вычислить: а) 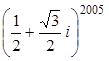 ; б)
; б) 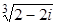 .
.
11. Восстановить аналитическую функцию 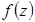 по ее действительной части
по ее действительной части 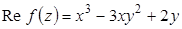 , если
, если 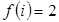 .
.
12. Функцию 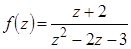 разложить в ряды Лорана в кольцах аналитичности.
разложить в ряды Лорана в кольцах аналитичности.
13. С помощью теоремы Коши о вычетах вычислить: а) 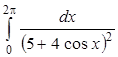 ; б)
; б) 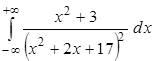 .
.
14. Разложить в тригонометрический ряд Фурье функции: а) 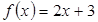 на
на 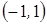 ; б)
; б) 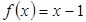 на
на  .
.
Раздел «Дифференциальные уравнения»
1. Построить последовательные приближения (нулевое, первое и второе) к решениям уравнений:
а) 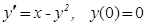
Ответ: 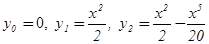
б) 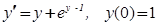
Ответ: 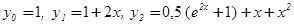
2. Указать какой-нибудь отрезок, на котором существует решение с данными начальными условиями:
а) 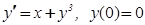
Ответ: – 0,5 ≤ х ≤ 0,5
б) 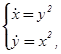 х (0) = 1, y (0) = 2
х (0) = 1, y (0) = 2
Ответ: – 0,1 ≤ х ≤ 0,1
3. Найти решение уравнения:
а) 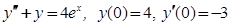
Ответ: 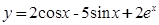
б) 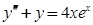
Ответ: y = C1cos x + C2sin x + (2 x – 2) ex
в) 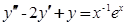
Ответ: 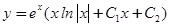
4. Исследовать на устойчивость по первому приближению тривиальное решение системы:
1) 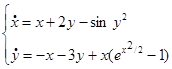 2)
2) 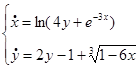 3)
3) 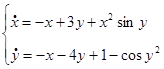
4) 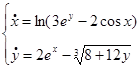 5)
5) 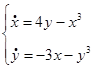 6)
6) 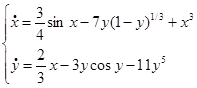
Раздел «Уравнения с частными производными»
1. Решить задачу
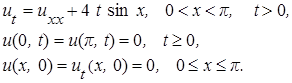
2. Решить задачу
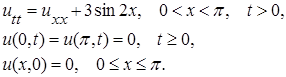
3. Решить задачу
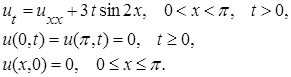
4. Решить задачу

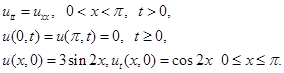
5. Решить задачу
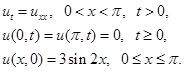
Раздел «Теория вероятностей»
1. В каждой из трех урн находится по 6 белых и 4 черных шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым
2. Стержень ломается случайным образом на две части. Каково среднее отношение длины короткого куска к длине длинного куска?
Раздел «Методы оптимизации»
1. Найти все базисные планы. Решить задачу симплекс-методом.
а) 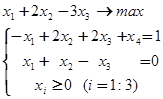 б)
б) 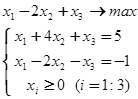
Ответ: базисные планы - Ответ: базисные планы –
(0; 0; 0; 1), (1; 0; 1; 0) (1; 1; 0) и (2; 0; 3)
и (0; ¼; ¼; 0)
2. Найти все стационарные точки:
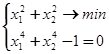
Ответ: (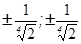 ), (0;
), (0; 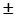 1); (
1); (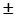 1; 0)
1; 0)
3. Решить задачи:
а) 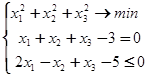 б)
б) 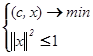
Ответ: (1; 1; 1) Ответ: 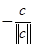
Раздел «Численные методы»
1. Для функции f (x) = x 3 – 3 x 2 + 4 x – 5 вычислить f ´(0) по симметричной формуле численного дифференцирования при h = 0.01.
2. Для функции f (x) = x 3 – 3 x 2 + 4 x – 5 вычислить f ″(0) по симметричной формуле численного дифференцирования при h = 0.01.
3. Доказать, что трехчленная симметричная формула численного дифференцирования для f ″(x о) имеет порядок погрешности О (h 2 ), если функция f (x) имеет ограниченную четвертую производную.
4. Найти правые части системы дифференциальных уравнений
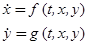
так, чтобы траектория (x (t), y (t)) c x (0) = 0, y (0) = 0 была развертывающейся
спиралью.
Раздел «Компьютерные науки»
1. Описать алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел (рекурсивный и итеративный варианты).
2. Описать процедуру обмена значениями двух переменных.
3. Имеется список имен: Alice, Byron, Carol, Diane, Elaine, Floyd, Gene, Henry, Iris. Какой алгоритм поиска (последовательный или бинарный): а) позволит найти быстрее имя Gene? б) позволит быстрее обнаружить отсутствие имени Bruce?
4. Предположим, что при использовании алгоритма сортировки методом вставки компьютеру требуется в среднем одна секунда для сортировки списка из 100 элементов. Оцените, сколько времени компьютеру понадобится для сортировки списка из 1000 элементов?
5. Докажите полноту следующих классов булевых функций:
а) { | } (| - штрих Шеффера);
б) { ↓ } (↓ - стрелка Пирса);
в) { 0,→ };
г) { 1, ×, +} (+ - сложение mod 2).
6. Докажите, что простой граф с n вершинами, степень каждой из которых не
менее  , является связным.
, является связным.
7. Пусть G = (V, E) – простой граф. Дополнением графа G называют простой граф
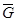 такой, что вершины
такой, что вершины 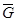 являются смежными тогда и только тогда, когда они
являются смежными тогда и только тогда, когда они
не смежны в G. Докажите, что один из графов G и 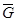 является связным.
является связным.
8. Пусть G = (V, E) – простой граф. Дополнением графа G называют простой граф
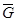 такой, что вершины
такой, что вершины 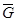 являются смежными тогда и только тогда, когда они
являются смежными тогда и только тогда, когда они
не смежны в G. Граф называется самодополнительным, если он изоморфен
своему дополнению. Докажите, что число вершин самодополнительного графа
представляется либо в виде 4 k, либо в виде 4 k + 1.
Литература
Дата добавления: 2015-08-17; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теория вероятностей и математическая статистика | | | Детские сухие бассейны |