Определение индуктивности КИ

Простейший индуктивностью является отрезок прямолинейного электрического проводника. Т.к. магнитное поле существует внутри и снаружи проводника, то можно выделить две составляющие индуктивности – внутреннюю (L_внутр.) и внешнюю (L_вн.). Полная индуктивность прямолинейного проводника с круглым сечением определяется по формуле:

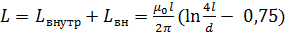= 0,002·Ɩ·(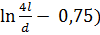

где 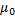– магнитная постоянная, равная 4π·10^-7 г/м;

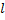– длина прямолинейного проводника;

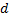– диаметр проводника.

Из формулы видно, что индуктивность такого проводника зависит только от его длины и диаметра провода.

Для инженера-конструктора важно знать, как влияет форма проводника на его индуктивность. Если взять проводник фиксированной длины и придавать ему разные формы, то индуктивность его будет разной (рис. 5.3), причем, наибольшую индуктивность имеет прямолинейный (незамкнутый) проводник.

Правило: Наибольшей индуктивностью обладает тот из замкнутых геометрических контуров одинакового периметра, который имеет наибольшую площадь.

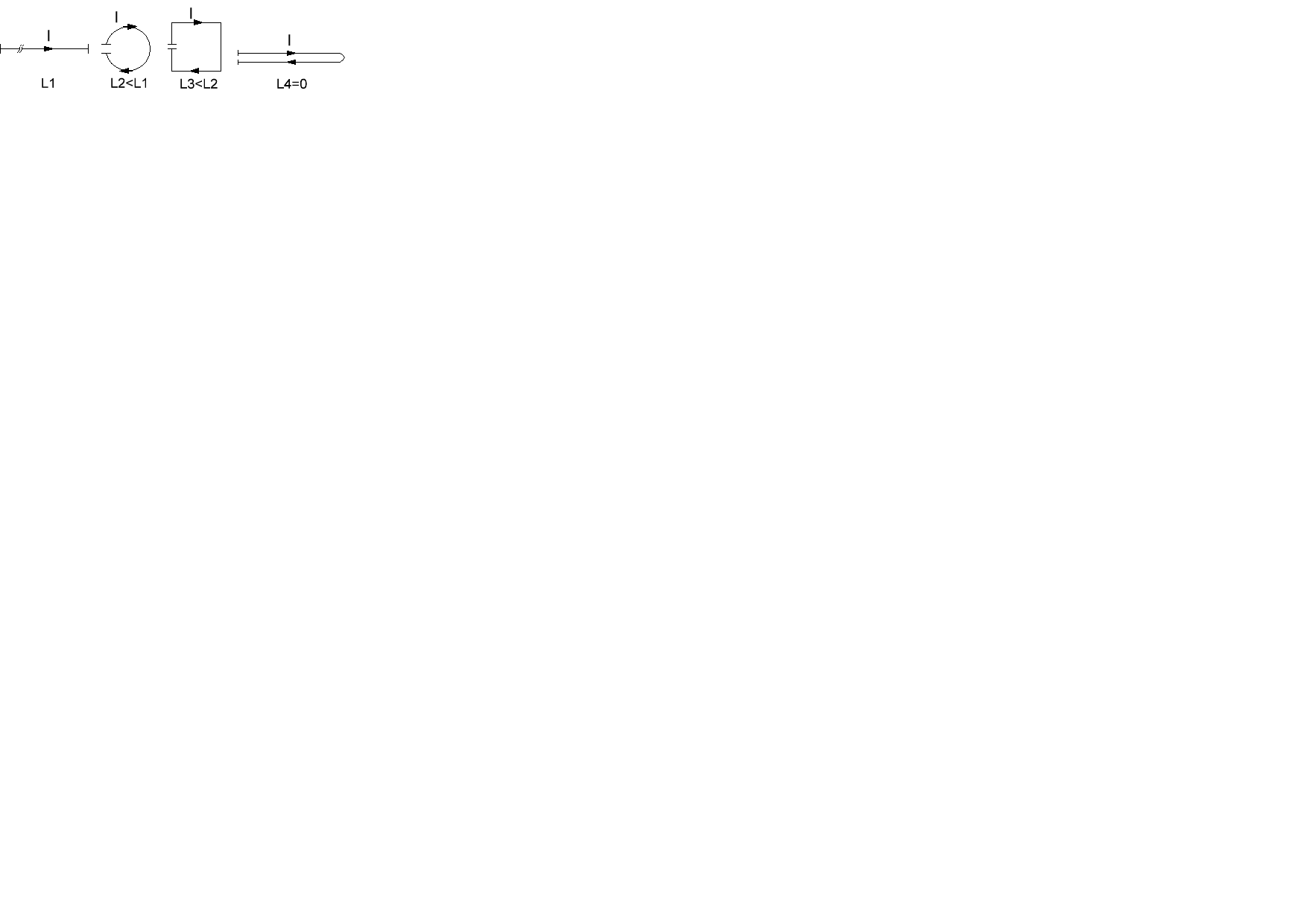
Рис. 5.3 – Влияние формы проводника на его индуктивность

Если же проводник свить в спираль, то его индуктивность значительно возрастет по сравнению с прямолинейным проводником, т.к. каждый виток будет находиться не только в своем магнитном поле, но и в поле соседних витков. В общем виде полная индуктивность спиральной катушки определяется выражением:

,

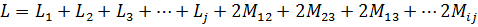где 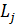– собственная индуктивность j-го витка;

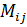– величина взаимоиндукции между i-м и j-м витками.

Индуктивность катушки, свитой из проводника диаметром d и длиной Ɩ, зависит от числа витков следующим образом

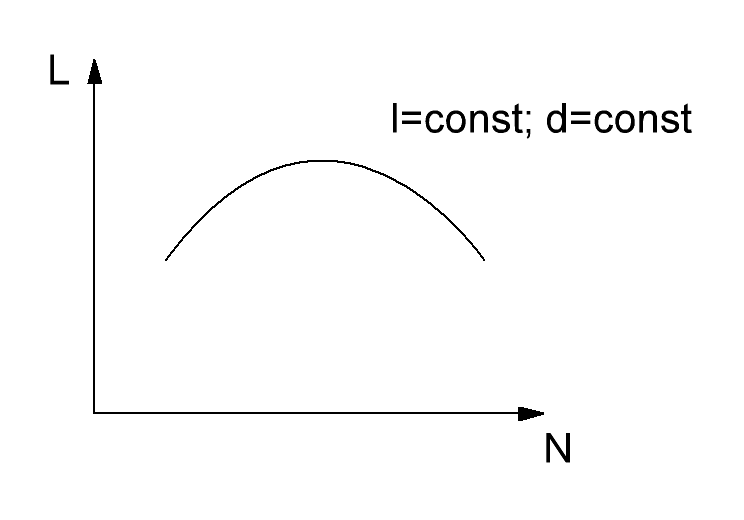
Индуктивность с увеличением числа витков N сначала растет, а затем снижается из-за уменьшения взаимной связи между удаленными витками.

Введение в КИ магнитного сердечника позволяет существенно увеличить ее индуктивность, либо при заданной индуктивности уменьшить размеры катушки индуктивности. В общем виде индуктивность КИ с сердечником определяется соотношением

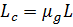
где 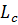- индуктивность КИ с сердечником,

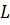- индуктивность той же катушки, но без сердечника,

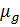- действующая магнитная проницаемость сердечника.

Величина 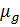зависит от магнитной проницаемости материала, частоты, конструкции сердечника, соотношений между геометрическими размерами катушки и сердечника:

,

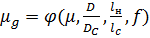где D – диаметр катушки;

D_С – диаметр сердечника;

Ɩ_Н – длина намотки провода;

Ɩ_С – длина сердечника;

f – частота.

Действующая магнитная проницаемость всегда меньше магнитной проницаемости материала, лишь в КИ на тороидальных сердечниках с равномерной обмоткой 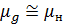, где 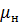–начальная магнитная проницаемость материала. Для характеристики системы использование магнитных свойств материала сердечника вводится коэффициент 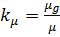. Для тороидальных сердечников 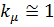, для других конструкций .

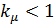Дата добавления: 2015-08-17