Проверка результатов синтеза

Определим запасы устойчивости и оценим качество переходных процессов в системе с корректирующим устройством. Для этого запишем выражение передаточной функции разомкнутой системы.

Предварительно введем в схему гибкую обратную связь, которой соответствует параллельное корректирующее устройство в виде дифференцирующего звена :

Рисунок 5. Схема с учетом всех корректирующих устройств

Рассмотрим случай, когда гибкой обратной связью охвачено колебательное звено второго порядка:

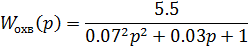
Тогда эквивалентная передаточная функция участка схемы, охваченного корректирующим устройством:

где

Найдем значение корректирующего коэффициента :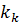

Также, учтем, что:

Тогда имеем:

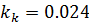
Таким образом:

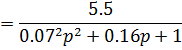
Переходной процесс в системе становится менее колебательным и превращается в апериодический, т.к .

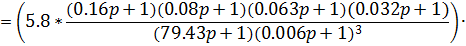
Построим логарифмические частотные характеристики, соответствующие данной передаточной функции:

Рисунок 6. Логарифмические частотные характеристики разомкнутой системы

Запас устойчивости по амплитуде составляет , что выше нормируемого значения 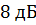. Запас устойчивости по фазе составляет:

Запас устойчивости по фазе больше нормируемого значения .

Из графика определим частоту среза:

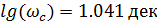
Оценим время переходного процесса:

Полученное время получилось меньше заданного, что говорит о том, что система имеет хорошие регулировочные характеристики.

Для оценки перерегулирования построим вещественную частотную характеристику замкнутой системы:

Таким образом, делаем вывод, что рассматриваемая система имеет запас устойчивости по амплитуде (), также время переходного процесса меньше заданного предела ().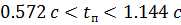

Касаемо запаса устойчивости по фазе: запас устойчивости больше нормируемого значения (). Перерегулирование имеет меньшее значение, чем нормируемое ().

Дата добавления: 2015-08-17