Паспорт комплекта тестовых заданий

Утверждаю

Директор института

_________ Абдыгаппарова С.Б.

«___» февраля 2014 г.

Паспорт комплекта тестовых заданий

для экзаменационного тестирования

по дисциплине Информтизация экономических расчетов

(наименование дисциплины)

для студентов специальности 5В050800-Учет и аудит _

(шифр и наименование специальности)

в количестве 8 человек

Институт	Экономики и бизнеса
Кафедра	Логистика и оценка
Курс
Семестр
Количество кредитов
Количество тестовых вопросов

Зам. директора института по УР:	___________________ Дильдебаева Ж.Т.
Заведующий кафедрой:	____________________ Чакеева К.С.
Составитель:	___________________ Ахметкалиева С.К.
Ответственное лицо за прием КТЗД:	_____________

Алматы 2014

$$$1

Для определения любой переменной в Mathcad в первую очередь нужно:

A) напечатать имя переменной, которую нужно определить;

B) ввести значение переменной;

C) войти в символьный процессор;

D) установить вставку шаблонов;

E) поместить курсор ниже предыдущих строк.

$$$2

Для ввода символа определения(присвоения) любой переменной в Mathcad в первую очередь нужно:

A) на панели калькулятора Mathcad выбрать :=;

B) напечатать двоеточие и запятую;

C) Shift +:

D) набрать точку с клавиатуры;

E) на панели калькулятора выбрать символ - /.

$$$3

Для определения дискретной переменной в Mathcad в первую очередь нужно:

A) ввести дискретную переменную и определить (присвоить) диапазон изменения с указанием шага при помощи шаблона m..n на панели калькулятор;

B) установить начальное значение дискретного аргумента;

C) щелкнуть мышкой на значении в определении дискретного аргумента;

D) определить диапазон;

E) определить шаг изменения дискретного аргумента

$$$4

Шаблон m..n на панели калькулятор служит для:

A) ввода дискретного аргумента;

B) ввода конечного значения дискретного аргумента;

C) указанияшага изменения дискретного аргумента;

D) указания начального значения дискретного аргумента;

E) указания последнего значение присваиваемое дискретному аргументу.

$$$5

Если задан дискретный аргумент t из диапазона (–10, 10) с шагом изменения 0.2, то в Mathcad следует сделать следующий набор:

A) t:= -10, -9.8..10

B) t:= -10, 10.8..10

C) t:= -10, 10.2..10

D) t:= -10, -9.8:10

E) t:= -10, -9.8;10

$$$6

Если шаг изменения дискретного аргумента равен 1, то достаточно выбрать:

A) шаблон m..n на панели калькулятор;

B) ввести шаг изменения дискретного аргумента;

C) напечатать символ-;

D) напечатать символ- &

E) вместо m поставить 1.

$$$7

Если шаг изменения дискретного аргумента отлично от 1, то достаточно выбрать:

A) шаблон m..n на панели калькулятор, затем после начального значения дискретного аргумента поставить запятуюиустановить число с учетом шага изменения;

B) ввести шаг изменения дискретного аргумента;

C) напечатать символ-;

D) вместо m поставить 0;

E) вместо m поставить 1.

$$$8

Для ввода формулы s x h в первую очередь нужно:

A) определить переменные s и h;

B) определить формулу s x h;

C) напечатать символ – «; «

D) введем действие умножения с панели калькулятор;

E) определить формулу для S.

$$$9

Точка с запятой с клавиатуры для Mathcad при определении дискретного аргумента служит:

A) для определения последнего значения дискретного аргумента;

B) для определения второго значения дискретного аргумента

C) для определения переменных;

D) для указания диапазона дискретного аргумента;

E) для определения предпоследнего значения дискретного аргумента.

$$$10

Для определения функции в первую очередь нужно:

A) напечатать f(x):=

B) набрать шаблон для дроби

C) определить дробь;

D) набрать sin(x)/x;

E) набрать sin(x).

$$$11

Одним из методов решения нелинейного уравнения является:

A) метод половинного деления (метод бисекции);

B) метод Гаусса;

C) метод трапеций;

D) метод Симпсона;

E) метод Рунге-Кутта.

$$$12

Одним из методов решения линейного уравнения является:

A) метод Гаусса;

B) метод половинного деления (метод бисекции);

C) метод трапеций;

D) метод Симпсона;

E) метод Рунге-Кутта.

$$$13

Одним из методов решения нелинейного уравнения является:

A) метод простой итерации;

B) метод Гаусса;

C) метод трапеций;

D) метод Симпсона;

E) метод Рунге-Кутта.

$$$14

Одним из методов решения нелинейного уравнения является:

A) метод Ньютона;

B) метод Гаусса;

C) метод трапеций;

D) метод Симпсона;

E) метод Рунге-Кутта.

$$$15

Приближенным методом вычисления определенного интеграла является:

A) метод Симпсона;

B) метод Гаусса;

C) метод Ньютона;

D) метод касательных;

E) метод Рунге-Кутта.

$$$16

Приближенным методом вычисления определенного интеграла является:

A) метод трапеций;

B) метод Гаусса;

C) метод Ньютона;

D) метод касательных;

E) метод Рунге-Кутта.

$$$17

Одним из методов решения системы линейного уравнения является:

A) метод Зейделя;

B) метод касательных;

C) метод трапеций;

D) метод Симпсона;

E) метод Рунге-Кутта.

$$$18

Аппроксимация таблично заданных функций осуществляется:

A) методом наименьших квадратов;

B) методом половинного деления (метод бисекции);

C) методом трапеций;

D) методом Симпсона;

E) методом Рунге-Кутта.

$$$19

В методе наименьших квадратов в качестве аппроксимирующих функций используют многочлен вида:

A)

B)

C)

D)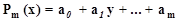

E)

$$$20

Если функция f(x)=0 определена на [a,b] f(a)>0, f(b)>0, то:

A) на данном отрезке решения не существует;

B) внутри отрезка [a,b] содержится по меньшей мере один корень уравнения;

C) методом половинного деления можно построить множество вложенных отрезков;

D) f ¢(x)=0 существует и сохраняет постоянный знак;

E) на отрезке [a,b] существует два действительных корня.

$$$21

Если функция f(x)=0 определена на [a,b] f(a)>0, f(b)<0, то:

A) внутри отрезка [a,b] содержится по меньшей мере один корень уравнения;

B) внутри отрезка [a,b] не существует корня;

C) точка х=а является корнем уравнения;

D) f ¢(x)=0 существует и сохраняет постоянный знак;

E) на отрезке [a,b] корней нет.

$$$22

Если функция f(x)=0 определена на [a,b] f(a)>0, f(b)<0,f([a+b]/2)<0, то рассматриваем отрезок:

A) [a, (a+b)/2];

B) [a/2, b];

C) (- µ, a);

D) (- µ, µ,);

E) на отрезке [a,b/2].

$$$23

Если функция f(x)=0 определена на [a,b] f(a)<0, f(b)>0, f([a+b]/2)<0, то рассматриваем отрезок:

A) [ (a+b)/2, b]

B) [a, c) [a/2, b]

C) (- µ, a)

D) (- µ, µ,)

E) на отрезке [a,b/2]

$$$24

Один из этапов математического моделирования:

A) свойства среды;

B) естественный элемент;

C) полнота экономической модели;

D) макроэкономическая модель;

E) технология моделирования.

$$$25

Один из этапов математического моделирования:

A) экономический объект;

B) цель исследования;

C) выявление существенных факторов;

D) разработка методов;

E) технология моделирования.

$$$26

Один из этапов математического моделирования:

A) экономическая модель;

B) решение уравнения при различных значениях параметра;

C) вычислительный алгоритм;

D) выбор языка программирования;

E) разработка методов.

$$$27

Один из этапов математического моделирования:

A) математическая модель;

B) некоторая «теоретическая копия»;

C) принятие правильных решений;

D) законы развития данного объекта;

E) технология моделирования.

$$$28

Одним из методов решения нелинейного уравнения является:

A) метод касательных;

B) метод Гаусса;

C) метод трапеций;

D) метод Симпсона.

E) метод Рунге-Кутта

$$$29

Один из этапов математического моделирования:

A) программная реализация;

B) полнота экономической модели;

C) выбранный вычислительный алгоритм;

D) технология моделирования;

E) метод Рунге-Кутта.

$$$30

Один из этапов математического моделирования:

A) алгоритм решения;

B) изучение поведения, входящих в нее уравнения;

C) точность приближенных решений;

D) применение численных методов;

E) технология моделирования.

$$$31

Один из этапов математического моделирования:

A) завершающий;

B) прогнозирование;

C) количественная форма практических реализаций;

D) технология моделирования;

E) численные методы.

$$$32

Одна из составляющих схемы вычислительного алгоритма:

A) численные методы;

B) экономическая ситуация;

C) точная количественная форма модели;

D) анализ результатов;

E) отыскание промежуточных значений функции.

$$$33

Одна из составляющих схемы вычислительного алгоритма:

A) аппроксимация и интерполяция функций;

B) отыскание промежуточных значений функции;

C) табличные значения функции;

D) нумерация узлов;

E) экономическая ситуация.

$$$34

Одна из составляющих схемы вычислительного алгоритма:

A) итерационные методы решения нелинейных уравнений;

B) постановка задачи;

C) локализация корней;

D) сходимость итерационных процессов;

E) экономическая ситуация.

$$$35

Одна из составляющих схемы вычислительного алгоритма:

A) прямые и итерационные методы решения систем линейных уравнений;

B) конечное число действий;

C) последовательность приближений;

D) метод последовательного исключения неизвестных;

E) нумерация узлов.

$$$36

Одна из составляющих схемы вычислительного алгоритма:

A) численное дифференцирование;

B) аналитическое дифференцирование;

C) задание функции таблицей;

D) конечное число действий;

E) нумерация узлов.

$$$37

Одна из составляющих схемы вычислительного алгоритма:

A) численное интегрирование;

B) выражение интеграла через элементарные функции;

C) набор подгоночных параметров;

D) квадратурная форма;

E) табличное задание функции.

$$$38

Метод наименьших квадратов это:

A) приближение таблично заданной функции многочленами определенной степени;

B) табличное задание функции;

C) нахождение экстремума функции;

D) определение исходной системы уравнений третьей степени;

E) аналитическое задание функции.

$$$39

Метод решения нелинейных уравнений:

A) метод бисекции;

B) итерационный метод;

C) прямой метод;

D) метод Гаусса;

E) метод Симпсона.

$$$40

Один из этапов общий для всех итерационных процедур:

A) преобразование исходной системы уравнений;

B) обратный ход;

C) нулевой коэффициент на главной диагонали;

D) определить вектор-столбец неизвестных;

E) свойства среды экономического объекта.

$$$41

Один из этапов общий для всех итерационных процедур:

A) задание начального приближения;

B) определение вектора правых частей;

C) последовательность приближений;

D) обратный ход;

E) прямой ход.

$$$42

Один из этапов общий для всех итерационных процедур:

A) критерий окончания;

B) определение вектора правых частей;

C) определение нулевых коэффициентов на главной диагонали;

D) определение квадратной матрицы;

E) обратный ход.

$$$43

Один из этапов общий для всех итерационных процедур:

A) сходимость итерационного процесса;

B) приближенное решение;

C) конечное число итераций;

D) окончание итерационного процесса;

E) последовательность приближений;

$$$44

Метод решения систем линейных уравнений –это:

A) метод Гаусса;

B) метод Ньютона;

C) метод секущих;

D) метод бисекции;

E) метод трапеций.

$$$45

Алфавит входного языка Mathcad:

A) имена встроенных функций, спецзнаки;

B) малые и большие латинские и греческие буквы;

C) оператор, системные переменные;

D) big number;

E) идентификаторы, константы.

$$$46

Укрупненные элементы языка:

A) типы данных, операторы, функции, управляющие структуры;

B) идентификаторы, константы, функции;

C) математические операторы, числовые константы, масивы;

D) имена встроенных функций, спецзнаки;

E LONG NUMBER

$$$47

Машинная бесконечность в системе Mathcad:

A) 10³⁰⁷

B) 10³⁸

C) 10²⁵⁵

D) big number

E) LONG NUMBER

$$$48

Укажите правильную запись числа 0,001:

A) 0.001

B) 0,001

C) 0.001*10³

D) 0,001*10^-2

E) 1,0 * 10^-2

$$$49

В Mathcad дробная часть числа отделяется знаком:

A)точка;

B)запятая;

C)двое точие;

D)пользователь устанавливает по своему усмотрению;

E) зависит от стандарта ОС.

$$$50

Оператор локального присвоения имеет вид:

A): =

B) =

C)

D)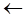

E)

$$$51

Глобальное присваивание осуществляется:

A)

B) =

C): =

D):

E)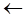

$$$52.

Чем отличаются обычные переменные от системных:

A) обычные переменные должны быть определены пользователем хотя бы однажды;

B) в них нет отличия;

C) обычные переменные определьяется через системных переменные;

D) обычные переменные определяются ОС;

E) идентификаторами.

$$$53

Оператор вывода значений:

A) =

B)

C)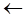

D)

Е): =

$$$54

Шаблон ранжирования переменных:

A) Name: =Nbegin, (Nbegin+Step)..Nend;

B) Name: = Nbegin, Step.. Nend;

C) Name: = Nbegin.., Step, Nend;

D) Name: = Nbegin, (Nbegin+ Step), Nend;

E) Name: = Nbegin,(Nbegin+Step).. Nend.

$$$55.

Укажите результат логического оператора 4>2=:

A) 1;

B) 0;

C) истина;

D) ложь;

E) 2.

$$$56. Укажите результат логического оператора 3*(4>2)=:

A) 3;

B) 0;

C) 6;

D) 1,5;

E) ложь.

$$$57

Укажите результат логического оператора 3*(4<2)=:

A) 0;

B) 3;

C) 6;

D) ложь;

E) истина.

$$$58

Какое действия объявить идентификатору z =5?

A) z 5;

B) z =5;

C) z: =5;

D) z 5;

E) z 5.

$$$59

Для решения квадратного уравнения используется встроенная функция:

A) polyroots;

B) isolve;

C) root;

D) solving;

E) given.

$$$60

Для вывода решения системы линейных уравнений используется встроенная функция:

A) isolve;

B) root;

C) polyroots;

D) solving;

E) given;

$$$61

Для решения системы нелинейных уравнений используется встроенные функции:

A) given, find;

B) root,find;

C) polyroots, given;

D) solving, find;

E) expand, solving.

$$$62

Для решения системы линейных уравнений размерности mxn используется встроенная функция:

A) правильного ответа нет;

B) root;

C) polyroots;

D) solving;

E) given, find.

$$$63

Для ввода системы нелинейных уравнений используется встроенная функция:

A) given;

B) root;

C) polyroots;

D) solving;

E) expand.

$$$64

Для ввода коэффициентов системы линейных уравнений размерности nxn используется:

A) матрица размерности nxn

B) вектор –столбец размерности nx1;

C) вектор-строка размерности 1хn;

D) вектор –столбец транспонированная;

E) вектор-строка транспонированная;

$$$65

Для вывода решения системы нелинейных уравнений используется встроенная функция:

A) find;

B) given;

C) root;

D) polyroots;

E) expand

$$$66

Для ввода системы нелинейных уравнений вместо знака равенства используют:

A) Ctrl+ =;

B) =;

C): =;

D) ;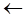

E) ;

$$$67

Для ввода коэффициентов свободных членов системы линейных уравнений используют:

A) вектор –столбец размерности nx1;

B) матрица размерности nxn

C) вектор-строка размерности 1хn;

D) вектор –столбец транспонированная;

E) вектор-строка транспонированная.

$$$68

Для ввода единичной матрицы в Mathcad используют встроенную функцию:

A) identity;

B) given;

D) root;

D) polyroots;

E) expand.

$$$69

Для того, чтобы нумерацию столбцов в матрице Mathcad воспринимала с 1 используют оператор:

A) ORIGIN:= 1;

B) BEGIN:=1;

C) FOR:= 1;

D) ARRAY:=1;

E) ORIGIN:=0.

$$$70

Для сдвига графика функции у= f(x) по оси абсцисс –ОХ влево нужно:

A) у= f(x-а);

B) у= f(x+а);

C) у= f(*а);

D) у= f(x/а);

E) у= а*f(x).

$$$71

Для сдвига графика функции у= f(x) по оси абсцисс –ОХ вправо нужно:

A) у= f(x+а);

B) у= f(x-а);

C) у= f(*а);

D) у= f(x/а);

E) у= а*f(x).

$$$72

Для сдвига графика функции у= f(x) по оси ординат –ОУ вверх нужно:

A) у= f(x)+в;

B) у= f(x+а);

C) у= f(*а);

D) у= f(x/а);

E) у= а*f(x).

$$$73. Для сдвига графика функции у= f(x) по оси ординат –ОУ вниз нужно:

A) у= f(x)-в;

B) у= f(x+а);

C) у= f(*а);

D) у= f(x/а);

E) у= а*f(x).

$$$74

Для растяжения или сжатия графика функции у= f(x) по оси ординат –ОУ нужно:

A) у= с_*f(x);

B) у= f(x+а);

C) у= f(_*а);

D) у= f(x/а);

E) у= а_*f(x).

$$$75

Для растяжения или сжатия графика функции у= f(x) по оси абсцисс –ОХ нужно:

A) у= f(а_* x);

B) у= f(x+а);

C) у= f(_*а);

D) у= f(x/а);

E) у= а_*f(x).

$$$76

При графическом способе отделения корня уравнения f(x)=0 определяют:

A) абсциссу точки пересечения графика у= f(x) с осью –ОХ;

B) ординату точки пересечения графика у= f(x) с осью –ОХ;

C) точку пересечения с началом координат (0,0);

D) точку пересечения на интервале (0, );

E) точку пересечения с началом координат (- ,0).

$$$77

Для решения нелинейного уравнения методом половинного деления в Mathcad используют оператор:

A) if;

B) for;

C) begin;

D) end;

E) array.

$$$78

Для решения нелинейного уравнения f(x)=0 на интервале (а,в) методом Ньютона:

A) необходимо, чтобы функция была определена, непрерывна и имела непрерывные производные на интервале;

B) необходимо, чтобы функция была определена на интервале;

C) необходимо, чтобы функция была непрерывна на интервале;

D) необходимо, чтобы функция имела непрерывные производные на интервале;

E) необходимо, чтобы функция была положительно определена на интервале.

$$$79

При решении уравнения f(x)=0 методом простых итераций уравнение приводят к виду:

A) ;

B) у= f(x+а);

C) у= f(_*а);

D) у= f(x/а);

E) у= а_*f(x).

$$$80

Интерполяция применяется для:

A) отыскания по заданным в виде таблицы значений функции у_i(x_i) неизвестных промежуточных значений функции у(х);

B) вычисления коэффициентов табулированной функции;

C) отыскания узловых точек;

D) вычисления значений функций;

E) вычисления значений функций в середине области определения функции.

$$$81

Одним из общих положений интерполяции является:

A) выбор узлов;

B) выбор многочлена;

C) выбор линейной комбинации алгебраических уравнений;

D) выбор экспоненциальных функций;

E) выбор линейной функции.

$$$82

Одним из общих положений интерполяции является:

A) выбор класса аппроксимирующих функций;

B) выбор многочлена;

C) выбор линейной комбинации алгебраических уравнений;

D) выбор экспоненциальных функций;

E) выбор линейной функции.

$$$83

Одним из общих положений интерполяции является:

A) выбор критерия близости;

B) выбор многочлена;

C) выбор линейной комбинации алгебраических уравнений;

D) выбор экспоненциальных функций;

E) выбор линейной функции.

$$$84

В методе трапеций узлы интерполяции:

A) известны заранее;

B) не определены;

C) находятся при помощи весовых коэффициентов;

D) определяются площадью криволинейной трапеции;

E) определяются площадью прямолинейной трапеции.

$$$85

Стандартная функция трапеций использует:

A) два узла на концах интервала;

B) три узла на заданном интервале;

C) четыре узла на заданном интервале;

D) пять узлов на заданном интервале;

E) один узел на заданном интервале.

$$$86

Вычисление интеграла по формуле Симпсона используют:

A) три узла на заданном интервале;

B) два узла на концах интервала;

C) четыре узла на заданном интервале;

D) пять узла на заданном интервале;

E) один узел на заданном интервале.

$$$87

Встроенная функция isolve используется для:

A) вывода вектора значений решения системы n-линейных уравнений с n-неизвестными;

B) вывода решения уравнения методом Ньютона;

C) вывода решения квадратного уравнения;

D) вывода решения уравнения методом бисекции;

E) интерполирования таблично заданной функции.

$$$88

Шаблон встроенной функции isolve имеет вид:

A) isolve (М, v), где М – матрица коэффициентов системы линейных уравнений, а v- вектор свободных коэффициентов системы;

C) isolve (М), где М – матрица коэффициентов системы линейных уравнений,

D) isolve (v), а v- вектор свободных коэффициентов системы;

D) isolve (М, v), М- вектор неизвестных системы линейных уравнений а v- вектор свободных коэффициентов системы;

Е) isolve (v), где v- вектор зависимых переменных.

$$$89

Встроенная функция polyroots используется для:

A) решения квадратного уравнения;

B) вывода решения уравнения методом Ньютона;

C) вывода решения уравнения n-ой степени;

D) вывода решения уравнения методом бисекции;

Е) интерполирования таблично заданной функции.

$$$90

Встроенная функция root используется для:

A) ввода шаблона s:= root (f(x),x);

B) вывода решения уравнения методом Ньютона;

C) вывода решения квадратного уравнения;

D) вывода решения уравнения методом бисекции;

Е) интерполирования таблично заданной функции.

$$$91

Встроенная функция Given используется для:

A) ввода системы нелинейных уравнений с использованием символического равенства - Ctrl =;

B) вывода решения уравнения методом Ньютона;

C) вывода решения квадратного уравнения;

D) вывода решения уравнения методом бисекции;

Е) интерполирования таблично заданной функции.

$$$92

Встроенная функция Given используется для:

A) ввода системы нелинейных уравнений;

B) вывода решения уравнения методом Ньютона;

C) вывода решения квадратного уравнения;

D) вывода решения уравнения методом бисекции;

Е) интерполирования таблично заданной функции.

$$$93

Встроенная функция find используется для:

A) вывода вектора решений системы нелинейных уравнений;

B) вывода решения уравнения методом Ньютона;

C) вывода решения квадратного уравнения;

D) вывода решения уравнения методом бисекции;

Е) интерполирования таблично заданной функции.

$$$94

Шаблон встроенной функция find имеет вид:

A) vec:= find(x,y,z);

B) vec:= (x,y,z)find;

C) x,y,z:= find;

D):= find

Е) vec= find.

$$$95

Встроенная функция minimize имеет следующий шаблон:

A) Q:= minimize (f, x, y);

B):= minimize (f, x, y)= Q;

C) minimize (f, x, y) Q:=;

D) (f, x, y)Q:= minimize;

Е) (f, x, y):= minimize.

$$$96

Встроенная функция minimize используется для:

A) вывода решения оптимизационных задач;

B) вывода решения уравнения методом Ньютона;

C) вывода решения квадратного уравнения;

D) вывода решения уравнения методом бисекции;

Е) интерполирования таблично заданной функции.

$$$97

Встроенная функция maximize используется для:

A) для решения оптимизационных задач;

B) вывода решения уравнения методом Ньютона;

C) вывода решения квадратного уравнения;

D) вывода решения уравнения методом бисекции;

Е) интерполирования таблично заданной функции.

$$$98

Встроенная функция maximize имеет следующий шаблон:

A) Q:= maximize (f, x, y);

B):= maximize (f, x, y)= Q;

C) maximize (f, x, y) Q:=;

D) (f, x, y)Q:= max;

Е) (f, x, y) Q:= maxi.

$$$99

Условием сходимости метода простой итерации является:

A) ;

B)

C) ;

D) ;

E) .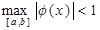

$$$100

В методе простой итерации для функции f(x)= x- sin(x)-1 в качестве итерирующей функции рассматриваем функцию:

A) ;

B) ;

C) :

D)

E)

Таблица 1

Темы тестовых вопросов по дисциплине «Информатизация экономических расчетов»

№	Наименование темы
	Встроенные функции Excel и Mathcad для решения экономических задач.
	Численные методы решения задач экономики
	Общие этапы итерационных процедур
	Метод наименьших квадратов
	Модель межотраслевого баланса
	Метод половинного деления
	Метод Ньютона
	Мее Методы информационного менеджмента
	Метод трапеции
	Метод золотого сечения
	Информатизация расчетов управления затратами
	Информатизация расчетов финансовой математики
	Информатизация расчетов оценки машин и оборудования
	Информатизация расчетов финансового учета
	Информатизация управления рабочим капиталом

Таблица 2 - Правильные ответы вопросов

Номер вопроса	Номер темы	Уровень сложности	Правильный ответ
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А
			А

Дата добавления: 2015-08-20