Векторное произведение

Сами того не подозревая, вы пользуетесь тензором второго ранга уже начиная с гл. 20 (вып. 2). В самом деле, мы опреде­лили там «момент силы, действующий в плоскости», например t_xy, следующим образом:

t _xy=xF_y-yF_x.

Обобщая это определение на три измерения, можно написать

t_ij=r_iF_j-r_jF_i. (31.22)

Как видите, величина t_ij — это тензор второго ранга. Один из способов убедиться в этом — свернуть t_ij с каким-то век­тором, скажем с единичным вектором е, т. е. составить

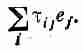
Если эта величина окажется вектором, то t _ij должен преобра­зовываться как тензор — это просто наше определение тензора. Подставляя выражение для t_ij, получаем

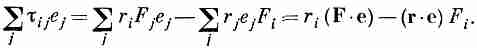
Поскольку скалярные произведения, естественно, являются скалярами, то оба слагаемых в правой части — векторы, как и их разность. Так что t_ij-— действительно тензор.

Однако t_ijпринадлежит к особому сорту тензоров, он антисимметричен, т. е.

t_ij=-t_ji.

Поэтому у такого тензора есть только три разные и неравные нулю компоненты: t_xy, t_yz и t_zz. В гл. 20 (вып. 2) нам удалось показать, что эти три члена почти «по счастливой случайности» преобразуются подобно трем компонентам вектора; поэтому мы могли тогда определить вектор

t=(t_x,. t_y, t_z) = (t_yz, t_zx, t_xy).

Я сказал «по случайности» потому, что это происходит только в трехмерном пространстве. Например, для четырех измерений антисимметричный тензор второго ранга имеет шесть различных ненулевых членов, и его, разумеется, нельзя заменить векто­ром, у которого компонент только четыре.

Точно так же как аксиальный вектор t == r X F является тен­зором, по тем же соображениям тензором будет и любое век­торное произведение двух полярных векторов. К счастью, они тоже представимы в виде вектора (точнее, псевдовектора), что немного облегчает нам всю математику.

Вообще говоря, для любых двух векторов а и b девять ве­личин a_ib_j образуют тензор (хотя для физических целей он не всегда может быть полезен). Таким образом, для вектора по­ложения r величины r_ir_jявляются тензором, а поскольку d_ij. тоже тензор, то мы видим, что правая часть (31.20) действитель­но является тензором. Подобным же образом тензором будет и (31.22), так как оба члена в правой части — тензоры.

Дата добавления: 2015-08-20