
Зам директора по персоналу фирмы «Компью-Нет» должен составить 6 пар-команд из техника-программиста и специалиста по маркетингу для работы по установке компьютерных сетей по индивидуальным требованиям клиентов. Пары составляются из вновь набранных сотрудников, среди которых проведен специальный психологический тест на взаимную совместимость. Индекс совместимости варьирует от 20 (выраженная враждебность) до 1 (возможность дружеских отношений), и для каждой потенциальной пары приведен в таблице.
| Аня | Маша | Катя | Лиза | Ольга | Софья | |
| Иван | ||||||
| Михаил | ||||||
| Павел | ||||||
| Николай | ||||||
| Алексей | ||||||
| Петр |
Можно ли так подобрать пары, чтобы ни один индекс совместимости не превышал 6?
Решение
В данном случае, учитывая что каждый из сотрудников должен быть
назначен только один раз (составляются пары), задачу можно сразу определить,
как задачу о назначениях. Так как количество программистов равно количеству
специалистов по маркетингу (их по шесть человек), то задача сбалансирована. По
условию задачи никаких запретов на составление определенных пар нет,
следовательно, эта задача не содержит никаких осложнений. Сначала скопируем таблицу данных и вставим ее чуть ниже по странице.
Выделим в ней область данных и сотрем их – в освобожденных ячейках, в данном
случае B11:G16, будут располагаться переменные задачи 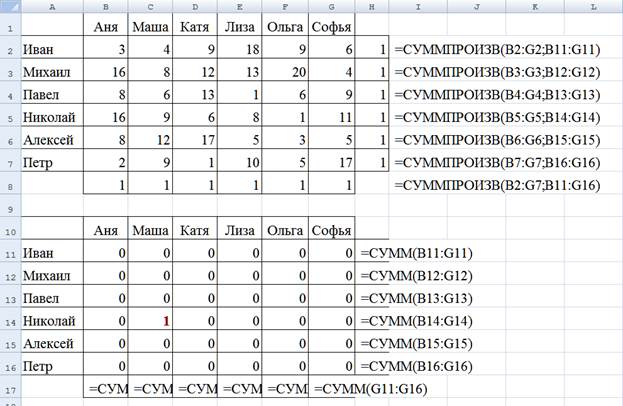
Для построения целевой функции, нужно рассчитать суммарный
индекс совместимости команд.Напишем в ячейку I8 формулу: =СУММПРОИЗВ(B2:G7;B11:G16).
Если в нижней таблице – таблице переменных B11:G16 – будут содержаться
только нули и шесть единиц, формирующих пары, результатом выполнения
функции станет сумма индексов совместимости для всех шести пар. При
показанном в таблице состоянии переменных результатом вычисления
функции будет число 9, на которое умножится единственная единица,
соответствующая паре Маша-Николай.
Если записать в ячейке I2 формулу =СУММПРОИЗВ(B2:G2;B11:G11), то
мы сможем вычислить индекс пары, которую техник-программист Иван составит
с кем-либо из специалистов по маркетингу. Протягивая формулу вниз, на ячейки
I3:I7, мы получим такие индексы для всех остальных пар, так как в каждую пару
обязательно входит один из техников-программистов.
Безусловно, можно было бы вычислять индексы и для пар, составляемых
специалистами по маркетингу с кем-либо из программистов. Для этого в строке
B9 нужно было ввести формулу =СУММПРОИЗВ(B11:B16;B2:B7), и протянуть
ее вправо. Результат, в смысле составляемых пар, в обоих случаях один и тот же. Вызываем Поиск решения и
указываем целевую ячейку – I8. Так как чем меньше индекс, тем лучше, в
качестве цели указываем поиск минимума. Переменные задачи B11:G16. В
параметрах обязательно указываем, что подразумевается линейная модель и что
переменные неотрицательны. Ограничений в задаче о назначениях, как и в
транспортных задачах, должно быть всего 2 (групповых). Ограничение
H11:H16=H2:H7 требует, чтобы каждый из техников-программистов был
назначен только один раз (столбец H2:H7 содержит только единицы), а
ограничение B17:G17=B8:G8 требует того же для специалистов по маркетингу. Суммарный индекс совместимости равен 19. Таблица переменных дает
распределение по парам: Иван-Аня, Михаил-Маша, Павел-Лиза, Николай-Ольга,
Алексей-Софья и Петр-Катя. 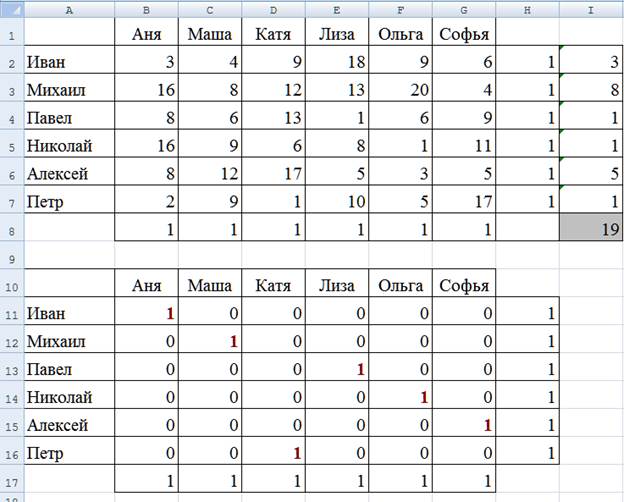
В полученном решении индексы совместимости пар принимают значения
от 1 до 8, где 8 и есть наихудший индекс среди всех пар. Получив
одно решение и запустив Поиск решения еще раз, не обнуляя переменные мы получаем новое решение. В этой задаче мы получаем два разных разбиения по парам, Попробуем потребовать, чтобы ни один индекс совместимости команд не
превышал 6: I2:I7<=6. Добавляем это ограничение в список Поиска решения и
запускаем на выполнение. Добавим условие, что все переменные – двоичные (0 или 1) и снова
попробуем решить задачу. В данном случае решение так же найдено и теперь удовлетворяет всем
нашим ожиданиям. Да, максимальный коэффициент 6. Да, все назначения либо 0,
либо 1. И, наконец, суммарный индекс выше, чем в оптимальном решении,
полученном нами ранее. 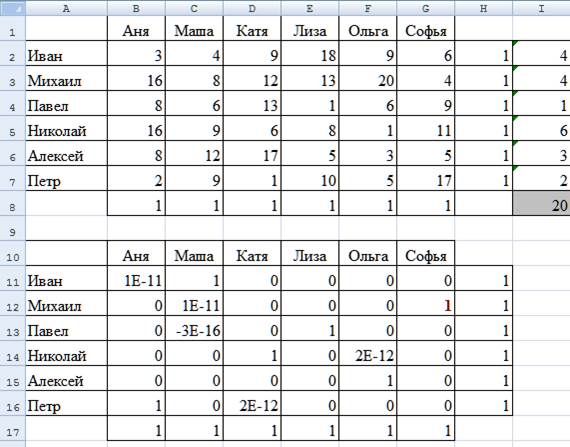
Дата добавления: 2015-08-20; просмотров: 254 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Поставки двух видов продуктов | | | Распределение аудиторов по фирмам |