Читайте также:
|
We will discard your results and expel you from the exam room in an indisputable way in case of violation of any rules 1)-5), written above.
Full list of theoretical questions for the final exam
(Your variant will contain exactly one question from this list. All your answers and solutions must be provided with detailed explanations! These questions are taken from our main textbook or have been explained during the lectures or seminars)
1. For the 2x2 matrices A,B,C their determinants |A| = 1, |B| = -3, |C| = 4. What is the determinant of the matrix A(B+C)? Why? Explain in details.
2. Which two of the following three conditions are equivalent:
a) The system Ax = 0 has only the trivial solution
b) det(A) = 0
c) Matrix A is invertible.
Explain in details.
3. Suppose that matrix B is invertible. Prove: AB ־ ¹ =B ־ ¹A if and only if AB=BA.
4. Prove that if {a,b,c} is linearly dependent set of vectors in a vector space V, and d is any vector in V, then { a,b,c,d } is also linearly dependent.
5. Prove, that if 
, then the reduced row-echelon form of
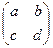is 
.
6. Prove the following theorem:
Any square matrix B can be represented in the form B=S+A, where S is symmetric, and A is anti-symmetric matrices. This representation is unique.
7. Give an example of inconsistent linear system, which has more unknowns than equations.
8. Give an example of 2x2 matrices A and B such that 
9. Prove that, if A and B are square matrices such that 
, then
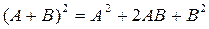
10. Let A be a square matrix, and I be identity matrix. Prove that for any natural number n
, if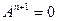 
11. Suppose that A and B are nxn matrices. Prove that
tr(AB) = tr(BA)
12. Let u, v, and w be nonzero vectors in 3-space with the same initial point, but such that no two of them are collinear. Prove that the vector u x(v x w) lies in the plane determined by v and w. Here the sign “x” denotes cross product.
13. Prove the Cauchy’s inequality, i.e. the absolute value of the inner product is not greater, than the product of the norms: |(u,v)| ≤||u||∙||v||
14. Prove the generalized theorem of Pythagoras: if the vectors u and v are orthogonal, then ||u+v||² = ||u||² + ||v||²
15. Prove the triangle inequality in inner product space: ||u+v|| ≤ ||u|| +||v||
16. Prove the “parallelogram equality”: ||u+v||² + ||u-v||² = 2||u||² + 2||v||²
17. Suppose that for a linear system Ax = b we have rank(A) = 4 and rank(A|b) = 5, where (A|b) is the augmented matrix. Is the system consistent? Why?
18. Recall that that the trace of a square matrix A is the sum of the elements on the main (principal) diagonal. Prove that the characteristic equation of a 2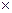 
2 matrix A can be expressed as
-tr(A) 
+det(A)=0,
where tr(A) is the trace of A.
19. Prove that if a vector u is orthogonal to both vectors v and w, then u is orthogonal to av+bw for all scalars a and b.
20. Find 
, if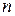 
is a positive integer and
.
21. Let
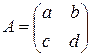
Show:
a) 
is diagonalizable, if 
.
b) is not diagonalizable, if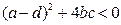 
.
22. Show that if is any 
matrix, then 
has an orthonormal set of 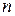eigenvectors.
23. Prove: if 
, then the matrix
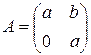
is not diagonalizable.
24. Use the Cayley-Hamilton theorem to calculate A 
for the matrix
. Explain the procedure in details.
25. Some 3x3 matrix A has the eigenvalues a= -2,b=2, c=3. Is the matrix A diagonalizable? Why?
26. Determine whether 
is a linear operator. Why? Explain in details.
Structure of the exam ticket.
The exam includes 8 tasks: 7 practical and 1 theoretical. Theoretical task is one of the questions listed above. For examples of the practical tasks, please look through your seminar and lecture note, and repeat corresponding parts of the textbook. A few samples are listed below.
Дата добавления: 2015-08-03; просмотров: 37 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Trying to take a picture or copy any exam material is strictly prohibited. | | | Cross and triple vector product |