Релятивистский закон сложения скоростей

Новым релятивистским представлениям о пространстве и времени соответствует новый закон сложения скоростей.

Запишем закон сложения скоростей для частного случая, когда тело М движется вдоль оси X' системы отсчета К', которая, в свою очередь, движется со скоростью υ ⃗ относительно системы отсчета К. Причем в процессе движения координатные оси X и X' все время совпадают, а координатные оси Y и Y', Z и Z' остаются параллельными (рис. 18.4).

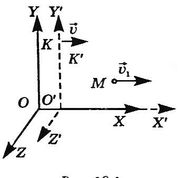Рис. 18.4

Обозначим модуль скорости тела относительно К' через υ 1 а модуль скорости этого же тела относительно К через υ 2. Тогда релятивистский закон сложения скоростей будет иметь вид

υ 2= υ 1+ υ 1+ υ 1 υc 2. (18.4)

Заметим, что формула (18.4) применима только в том случае, если все три вектора υ ⃗, υ ⃗ 1 и υ ⃗ 2 направлены вдоль одной прямой. В общем случае этот закон имеет более сложный вид. Однако при любой форме записи закона его сущность заключается в том, что скорость c света в вакууме является предельной скоростью передачи сигналов.

Действительно, пусть υ 1= c. Найдем скорость υ 2:

υ 2= c + υ 1+ cυc 2= c.

Предположим, что тело движется со скоростью υ 1= c относительно системы К', которая в свою очередь движется со скоростью υ = c относительно системы К. Тогда υ 2= c + c 1+ c ⋅ cc 2= c

Следовательно, при любых скоростях υ 1 и υ результирующая скорость υ 2 не превышает с.

Если υ ≪ c и υ 1≪ c, то членом υ 1 υc 2 знаменателе можно пренебречь и вместо (18.4) получим классический закон сложения скоростей

υ 2= υ 1+ υ.

Это согласуется с принципом соответствия, согласно которому новая физическая теория не отвергает целиком предшествующую теорию, она  указывает предел применимости старой теории.

Лоренцево сокращение длины Рассмотрим рисунок 8.5, на котором изображены две системы координат k и k'. Рис. 8.5 Пусть l ₀ = x '₂ – x '₂ – собственная длина тела в системе, относительно которого тело неподвижно (например: в ракете, движущейся со скоростью мимо неподвижной системы отсчета k (Земля)). Измерение координат x ₁ и x ₂ производим одновременно в системе k, т.е. t ₁ = t ₂ = t. Используя преобразования Лоренца, для координат получим: . Тогда

(8.4.6)

Формулы (8.4.6) описывают лоренцево сокращение длин. Собственная длина тела есть максимальная длина. Длина движущегося тела короче, чем покоящегося. Причем сокращается только проекция на ось x, т.е. размер тела вдоль направления движения.

Сокращение длин возникает из-за свойств псевдоевклидовой геометрии пространства Минковского, аналогичных удлинению сечения, например, цилиндра, когда оно проводится не строго поперёк оси, а косо. См. преобразования Лоренца.

Дата добавления: 2015-08-02