Индексный метод является одним из самых распространенных методов статистического анализа экономических явлений. 2 страница

цепные индексы с постоянными весами:

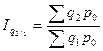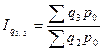; ; и т.д.; (8.51)

Переменные веса, как правило, веса отчетного (текущего) периода, обычно берутся при построении системы индексов качественных показателей.

Так, система агрегатных индексов цен имеет следующий вид:

Базисные индексы с переменными весами:

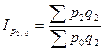; ; и т.д.; (8.52)

цепные индексы с переменными весами:

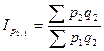; ; и т.д.; (8.53)

Аналогично строятся системы цепных и базисных индексов с переменными и постоянными весами и для других показателей.

Задача 4. Рассмотрим расчет системы агрегатных базисных и цепных индексов с постоянными и переменными весами на следующем условном примере:

Таблица 8.4. Динамика реализованной продукции и цен в универмаге города

Продукция	2003 г.	2004 г.	2005 г.
Объем продукции, тыс. шт., (q0)	Цена, тыс. ден. ед., (р0)	Объем продукции, тыс. шт., (q1)	Цена, тыс. ден. ед., (р1)	Объем продукции, тыс. шт., (q2)	Цена, тыс. ден. ед., (р2)
Пальто	1,2		1,4		1,7
Плащи	2,0		1,8		1,5
Куртки	2,5		2,8		3,3

Определим агрегатные базисные индексы физического объема реализованной продукции с постоянными весами (в ценах 2003 г.).

, или 107,1%;

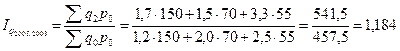, или 118,4%.

Определим агрегатные цепные индексы цен с переменными весами:

, или 112,3%;

, или 108,6%.

Многофакторные индексы. Индексный метод позволяет определить влияние не только двух, а любого числа факторов, формирующих сложное явление (результативный показатель). Если результативный фактор можно представить как последовательное произведение двух и более отдельных факторов, то такая связь называется мультипликативной. Например, производительность труда одного рабочего за месяц (среднемесячная выработка, у) равна его среднечасовой выработке (а), умноженной на среднее число отработанных часов за смену (среднюю продолжительность рабочего дня, b) и на среднее число отработанных за месяц дней (среднюю продолжительность рабочего месяца, с). Получаем следующую трехфакторную модель:

(8.54)

А так как между индексами показателей существует такая же связь, как и между самими показателями, то

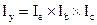(8.55)

Решение индексных мультипликативных моделей зависит от того, с какого фактора, экстенсивного или интенсивного, начинается произведение факторов-сомножителей в исследуемой модели:

а) если система взаимосвязи факторов начинается с интенсивного (качественного) показателя «а», то еще не рассмотренные факторы берутся на уровне отчетного периода, а уже рассмотренные остаются на уровне базисного периода.

(8.56)

б) если система взаимосвязи факторов начинается с экстенсивного (количественного) показателя «а», то еще не рассмотренные факторы берутся на уровне базисного периода, а уже рассмотренные – на уровне отчетного периода:

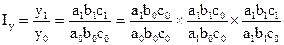(8.57)

Чтобы определить абсолютное изменение результативного показателя в целом , нужно от числителя его индекса вычесть знаменатель:

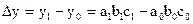(8.58)

Общее абсолютное изменение результативного показателя равно сумме абсолютных изменений за счет влияния всех исследуемых факторов, формирующих это явление:

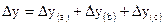(8.59)

Расчеты абсолютных изменений результативного показателя за счет изменения каждого показателя-фактора по каждой модели можно произвести двумя способами:

1) Разностным методом:

а) на первом месте фактор «а» - интенсивный показатель, тогда:

(8.60)

(8.61)

(8.62)

б) на первом месте фактор «а» - экстенсивный показатель, - тогда:

(8.63)

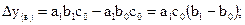(8.64)

(8.65)

2) упрощенным способом (с помощью индексов):

а) фактор «а» - интенсивный показатель, тогда:

(8.66)

(8.67)

(8.68)

б) фактор «а» - экстенсивный показатель, тогда:

; (8.69)

(8.70)

(8.71)

Рассмотрим на условном примере технику решения трехфакторной мультипликативной индексной модели.

Задача 5. Имеются следующие данные о среднемесячной выработке продукции за два периода:

Таблица 8.5.

Показатель	Условное обозначение	Базисный период	Отчетный период
Средняя часовая выработка одного рабочего, деталей	а
Средняя фактическая продолжительность рабочего дня, час	b	7,8	7,5
Средняя фактическая продолжительность рабочего месяца, дней	с	23,5	24,8
Средняя месячная выработка одного рабочего, деталей	у = abc

Индекс результативного фактора (у) - средней месячной выработки одного рабочего равен:

Абсолютный прирост равен:

Следовательно, среднемесячная выработка одного рабочего в отчетном периоде по сравнению с базисным увеличилась на 1998 деталей, или на 9,1%.

Рассчитаем, как влияли на это изменение в абсолютном и относительном выражении отдельные факторы, отметив предварительно, что модель начинается с интенсивного фактора (а) – среднечасовой выработки одного рабочего. Расчеты произведем двумя методами:

I разностным методом:

­– фактор а:

– фактор b:

– фактор с:

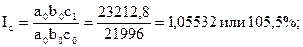
II с помощью индексов

Результаты расчетов обоими методами дали одинаковые результаты.

Общий абсолютный прирост равен сумме абсолютных приростов по всем факторам, т.е.

А индекс результативного показателя равен произведению индексов факторных показателей, т.е.

Таким образом, средняя месячная выработка одного рабочего в отчетном периоде по сравнению с базисным увеличилась на 1998 деталей, или на 9,1%. В том числе за счет роста средней часовой выработки одного рабочего на 7,5%, средняя месячная выработка увеличилась на 1674 детали, за счет роста средней фактической продолжительности рабочего месяца на 5,5% - на 1216,8 детали, а за счет снижения средней фактической продолжительности рабочего дня на 3,8% средняя месячная выработка одного рабочего снизилась на 892,8 деталей.

В данном примере дан анализ трех факторов, влияющих на результативный показатель. Модель строилась, начиная с интенсивного фактора. Аналогично можно произвести разложение сложного результативного показателя на любое число факторов-сомножителей. Но если модели строились, начиная с экстенсивного фактора, расчеты нужно производить по другой описанной выше методике.

Территориальные индексы характеризуют соотношение социально-экономических явлений в пространстве (по районам, областям, городам и т.п.). При построении агрегатной формы территориальных индексов возникает вопрос о том, какие показатели следует в этих индексах принимать в качестве весов или соизмерителей.

В теории и практике статистики предлагаются различные методы построения общих территориальных индексов.

Так, при построении агрегатных территориальных индексов качественных показателей в качестве весов используют «стандартизированные веса». В качестве их можно, например, взять соответствующие количественные показатели по республике или стране, либо по двум сравниваемым территориям А и Б вместе (Q), где

Q=q_a+q_b; (8.72)

(8.73)

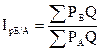(8.74)

Произведение и равно единице, т.е.

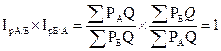(8.75)

Отсюда, (8.76)

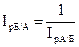(8.77)

Другим способом является сравнение индексируемого качественного показателя одной территории со средневзвешенной этого показателя по двум анализируемым территориям:

и (8.78)

, (8.79)

где (8.80)

Рассмотрим методику расчета территориальных индексов на следующем условном примере

Задача 8.6. Имеются следующие условные данные

Таблица 8.6. Продажа товаров на рынках двух районов

Наименование товара	Район А	Район Б
Цена единицы изделия, тыс. ден. ед. (рА)	Количество проданных единиц (qA)	Цена единицы изделия, тыс. ден. ед. (рБ)	Количество проданных единиц (qБ)
Изделие 1
Изделие 2
Изделие 3

Рассчитаем агрегатные территориальные индексы цен по двум районам.

I способ

, или 90,5%, т.е. средняя цена в районе А ниже, чем в районе Б на 9,5% (90,5% - 100% = - 9,5%)

, или 110,5%, т.е. средняя цена в районе Б выше, чем в районе А на 10,5% (110,5% - 100% = 10,5%)

II способ

Сначала рассчитаем средние цены по каждому изделию по двум районам:

тыс. ден. ед.

тыс. ден. ед.

тыс. ден. ед.

, или 96,1%, т.е. в районе А средняя цена ниже, чем в районе Б на 3,9% (96,1% - 100% = -,9%)

, или 106,0%, т.е. в районе Б средняя цена выше, чем в районе А на 6,0% (106% - 100% = 6,0%).

Построение агрегатных территориальных индексов количественных показателей также имеет свою особенность. Здесь в качестве весов в зависимости от целей анализа, от поставленной экономической задачи берутся соответствующие средние показатели отдельных элементов, исчисленные либо по обоим сравниваемым территориям, либо по более широкой территории (области, республике).

, (8.81)

, (8.82)

Произведение этих индексов также равно единице:

(8.83)

Рассчитаем эти индексы по нашему примеру

, или 155,9%, т.е. количество проданных трех изделий в районе А больше, чем в районе Б на 55,9%.

, или 64,1%, т.е. количество проданных трех изделий в районе Б меньше, чем в районе А на 35,9%.

Произведение этих индексов также равно единице

Косвенный метод

При этом методе формулы для расчета территориальных индексов качественных показателей, например, цены, имеют следующий вид:

и наоборот (8.84)

, (8.85)

а для расчета территориальных индексов количественных показателей, например, физического объема, такой вид:

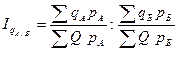и наоборот (8.86)

, (8.87)

где p и Q – стандартные значения.

Задачи

Задача 8.1. Имеются следующие данные о реализации овощей на рынке (табл. 8.7).

Таблица 8.7 Реализация овощей на рынках города

Овощи	Цена за 1 кг, ден. ед.	Продано, кг
II квартал	III квартал	II квартал	III квартал
Картофель Свекла Морковь	0,8 1,0 1,2	0,5 0,8 1,2

Определите:

1. Индивидуальные индексы цен и количества проданных овощей.

2. Общий индекс и абсолютное изменение стоимости реализованных овощей в III квартале по сравнению с первым.

3. Общий агрегатный индекс цен и абсолютное изменение выручки от реализации овощей за счет изменения цен.

4. Общий агрегатный индекс физического объема и абсолютное изменение выручки от реализации овощей за счет изменения количества проданных овощей.

5. Проверьте взаимосвязь рассчитанных индексов и сделайте выводы.

Задача 8.2. Имеются следующие данные об урожайности и посевной площади зерновых в хозяйстве (табл. 8.8):

Таблица 8.8 Динамика урожайности зерновых культур

Зерновые культуры	Базисный период	Отчетный период
урожайность, ц/га	посевная площадь, га	урожайность, ц/га	посевная площадь, га
Пшеница Озимая рожь Ячмень	24,5 26,0 21,3		32,0 30,5 26,4

Определите:

1. Индивидуальные индексы урожайности, посевных площадей и валового сбора по каждой культуре.

2. Общие агрегатные индексы урожайности, посевной площади и валового сбора.

3. Абсолютное изменение валового сбора в отчетном периоде по сравнению с базисным, в том числе за счет факторов (изменения урожайности и посевной площади).

4. Покажите взаимосвязь между исчисленными индексами и сделайте выводы.

Задача 8.3. Динамика себестоимости и объема производства продукции характеризуется следующими данными (табл. 8.9).

Таблица 8.9 Динамика себестоимости и объема производства продукции

Продукция	Выработано продукции, ед.	Себестоимость единицы продукции, млн. р.
Базисный период	Отчетный период	Базисный период	Отчетный период
Завод №1
АР-1			2,0	2,1
КС-20			3,2	3,6
Завод №2
КС-20			4,2	4,0

На основании имеющихся данных вычислите.

1. Для завода №1 (по двум видам продукции вместе):

а) общий индекс затрат на производство продукции;

б) общий индекс себестоимости продукции;

в) общий индекс физического объема производства продукции.

2.Определите в отчетном периоде по сравнению с базисным абсолютное изменение суммы затрат на производство продукции и разложите его по факторам (за счет изменения себестоимости и объема выработанной продукции).

3. Покажите взаимосвязь между исчисленными индексами.

4. Для двух заводов вместе (по продукции КС-20):

а) индекс себестоимости переменного состава;

б) индекс себестоимости постоянного состава;

в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.

5. Объясните различие между полученными величинами индексов постоянного и переменного состава.

6. Определите общее абсолютное изменение средней себестоимости единицы продукции в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней себестоимости и изменения структуры производства продукции.

Сформулируйте выводы.

Задача 8.4. Динамика средних цен и объема продажи на двух рынках города характеризуется следующими данными (табл.8.10).

Таблица 8.10 Динамика средних цен и объем продаж

Продукция	Продано продукции, тыс. кг	Средняя цена за кг, тыс. ден. ед.
базисный период	отчетный период	базисный период	отчетный период
Рынок №1
Картофель	4,0	4,2	0,64	0,76
Капуста	2,5	2,4	0,72	0,84
Рынок №2
Картофель	10,0	12,0	0,76	0,70

На основании имеющихся данных вычислите.

1. Для рынка №1 (по двум видам продукции вместе):

а) общий индекс товарооборота;

б) общий индекс цен;

в) общий индекс физического объема товарооборота;

2. Определите в отчетном периоде по сравнению с базисным абсолютный прирост товарооборота и разложите его по факторам (за счет изменения цен и объема продаж товаров).

3. Покажите взаимосвязь между исчисленными индексами.

4. Для двух рынков вместе (по картофелю):

а) индекс цен переменного состава;

б) индекс цен постоянного состава;

в) индекс влияния изменения структуры объема продаж картофеля на динамику средней цены.

5. Объясните различие между полученными величинами индексов постоянного и переменного состава.

6. Определите общее абсолютное изменение средней цены картофеля в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней цен и изменения структуры продажи картофеля.

Сформулируйте выводы.

Задача 8.5. Динамика себестоимости и объема производства продукции по двум предприятиям характеризуется следующими данными (табл.8.11).

Таблица 8.11. Динамика себестоимости и объема производства продукции

Продукция	Выработано продукции, тыс. ед.	Себестоимость единицы продукции, млн. р.
базисный период	отчетный период	базисный период	отчетный период
Предприятие №1
МД-5			5,0	5,8
МО-3			9,0	8,8
Предприятие №2
МД-5			7,0	7,5

На основании имеющихся данных вычислите:

1. Для предприятия №1 (по двум видам продукции вместе):

а) общий индекс затрат на производство продукции;

б) общий индекс себестоимости продукции;

в) общий индекс физического объема производства продукции.

2. Определите в отчетном периоде по сравнению с базисным абсолютное изменение суммы затрат на производство продукции и разложите его по факторам (за счет изменения себестоимости и объема выработанной продукции).

3. Покажите взаимосвязь между исчисленными индексами.

4. Для двух предприятий вместе (по продукции МД-5):

а) индекс себестоимости переменного состава;

б) индекс себестоимости постоянного состава;

в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.

5. Объясните различие между полученными величинами индексов постоянного и переменного состава.

6. Определите общее абсолютное изменение средней себестоимости единицы продукции в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней себестоимости и изменения структуры производства продукции.

Сформулируйте выводы.

Задача 8.6. Динамика средних цен и объема продажи на двух рынках города характеризуется следующими данными (табл.8.12.).

Таблица 8.12 Динамика средних цен и объеме продажи на двух рынках города

Продукт	Продано продуктов, ед.	Средняя цена за единицу, тыс. ден. ед.
базисный период	отчетный период	базисный период	отчетный период
Рынок №1
Молоко, л.			0,85	1,10
Творог, кг.			3,00	3,80
Рынок №2
Молоко, л.			0,80	0,96

На основании имеющихся данных вычислите.

1. Для рынка №1 (по двум видам продукции вместе):

а) общий индекс выручки от реализации продуктов;

б) общий индекс цен;

в) общий индекс физического объема проданных продуктов.

2. Определите в отчетном периоде по сравнению с базисным абсолютный прирост выручки от реализации продуктов и разложите его по факторам (за счет изменения цен и объема продажи продуктов).

3. Покажите взаимосвязь между исчисленными индексами.

4. Для двух рынков вместе (по молоку);

а) индекс цен переменного состава;

б) индекс цен постоянного состава;

в) индекс влияния изменения структуры объема продаж молока на динамику средней цены.

5. Объясните различие между полученными величинами индексов постоянного и переменного состава.

6. Определите общее абсолютное изменение средней цены молока в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней цен и изменения структуры продажи молока. Сформулируйте выводы.

Задача 8.7. Динамика себестоимости и объема производства продукции по двум заводам характеризуется следующими данными (табл.8.13).

Таблица 8.13 Динамика себестоимости и объема производства продукции

Продукция	Выработано продукции, тыс. ед.	Себестоимость единицы продукции, млн. р.
базисный период	отчетный период	базисный период	отчетный период
Завод №1
ОМ-95			3,0	3,3
КС-73			4,3	4,5
Завод №2
ОМ-95			4,0	4,2

На основании имеющихся данных вычислите:

Дата добавления: 2015-08-02