Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Течение газа с ударными волнами

АЭРОГАЗОДИНАМИКА | ОСНОВНЫЕ ГАЗОДИНАМИЧЕСКИЕ ПОНЯТИЯ. ОДНОМЕРНЫЕ ИЗОЭНТРОПИЧЕСКИЕ ТЕЧЕНИЯ ГАЗА. | ЗАДАЧИ. | ПРОФИЛЬ И КРЫЛО В ПОТОКЕ ИДЕАЛЬНОГО ГАЗА | ЗАДАЧИ. |


Читайте также:
  1. акие формулировки из нижеприведенных точно соответствуют ограничениям депутата законодательного (представительного) органа субъекта РФ в течение срока своих полномочий?
  2. аслаждение женщиной, у которой менструальный период, послеродовое очищение или кровотечение.
  3. более высокий уровень восприятия с помощью управления течением своих снов.
  4. В течение всех тех ужасных лет, когда я был курильщиком, я считал, что моя жизнь зависит от сигарет.
  5. В течение получаса мы молча шли вслед за ним. И как же велико было мое удивление, когда он привел нас к пещере или, скорее, к просторному гроту.
  6. Влияние вирусного гепатита «В» на течение беременности
  7. Влияние железодефицитной анемии на течение беременности, родов, состояние плода и новорожденного

Система уравнений для прямого скачка:

уравнение неразрывности ;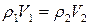

уравнение изменения количества движения ;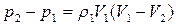

уравнение Бернулли .

Процесс перехода через фронт скачка адиабатический, поэтому 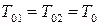и . Ударная адиабата (адиабата Гюгонио):

.

Соотношения между параметрами на прямом скачке уплотнения:

, , .

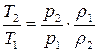Формула Прандтля или . Число Маха за прямым скачком .

Формула Рэлея .

Коэффициент восстановления полного давления

.

При переходе через косой скачок уплотнения (рис.6) касательная составляющая скорости не изменяется: Косой скачок – скачок нормальной к фронту скачка составляющей скорости. Соотношения для параметров течения при прямом скачке уплотнения (за исключением формулы для расчета ) применимы и для расчетов косого скачка при замене числа Маха на 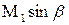. Скорости течения перед косым скачком уплотнения и за ним связаны простым соотношением:

.

Уравнение неразрывности для косого скачка . Отсюда с учетом рис.6

.

Формула Прандтля для косого скачка уплотнения: , где ; .

Углы поворота потока в косом скачке уплотнения и наклона фронта скачка связаны с числом Маха набегающего потока соотношением

.

ЗАДАЧИ

3.1. Прямые скачки уплотнения назад

54. Известны скорость V 1 = 500 м/с и температура Т 1 = 300 К потока воздуха перед прямым скачком уплотнения. Определить скорость V 2 и температуру Т 2 в потоке за скачком уплотнения.

55. Скорость потока воздуха перед прямым скачком уплотнения в 2 раза больше, чем за ним. Найти отношение температур Т 2 / Т 1 за скачком и перед ним.

56. Известны скорость V 1 = 800 м/с, давление p 1 = 105 Па и температура воздуха Т 1 = 300 К перед прямым скачком уплотнения. Найти скорость V 2, давление p 2 и температуру Т 2 за скачком уплотнения. Найти параметры торможения (давление p 0 и температуру Т 0) до скачка и после него.

57. Степень повышения статического давления в прямом скачке уплотнения p 2/ p 1 = 2,5. Определить Числа М1 до скачка и М2 после скачка, если показатель изоэнтропы k = 1,4.

58. Измерены статические давления перед прямым скачком p 1 = 0,5×105 Па и за ним p 2 = 1,2×105 Па. Найти давление изоэнтропического торможения перед прямым скачком p 01 и за ним p 02. Показатель изоэнтропы k = 1,4.

59. Сравнить увеличение плотности при ударном и изоэнтропическом сжатии воздуха, если в том и другом случаях давление возрастает в 10 раз. Объяснить разницу.

60. Температура воздуха в форкамере сверхзвуковой трубы Т 0 = 288 К. Поток на срезе сопла трубы имеет скорость V 1 = 530 м/с и обтекает препятствие с образованием прямого скачка. Найти V 2 - скорость воздуха после скачка.

61. Скорость воздуха, замеренная после скачка, V 2 = 280 м/с. Термопара в воздухе (рис.7) показала температуру + 77 °С. Найти температуру воздуха в потоке до скачка.

62. На прямом скачке плотность возросла в 2 раза. При каком числе l1 возник скачок уплотнения? Как изменится кинетическая энергия единицы объема газа на скачке?

63. При переходе воздуха через скачок уплотнения давление торможения уменьшилось в 5,2 раза, статическое давление увеличилось в 15 раз, температура увеличилась в 3,46 раза. Как изменится плотность потока и плотность заторможенного потока на скачке?

64. Воздух на расчетном режиме истекает из баллона, где он имеет температуру 16 °С, через сопло с отношением площадей выходного и критического сечений . Найти скорость, которую поток будет иметь, пройдя прямой скачок?

65. Давление, измеренное в сверхзвуковом потоке трубкой полного напора, в 12 раз больше давления, измеренного на щеке клина (рис.8). Найти коэффициент восстановления полного давления в прямом скачке.

66.

 
 

Рост плотности воздуха на скачке уплотнения составил 3,81 раза. Найти коэффициент восстановления полного давления на скачке.

67. Измерения в простом сверхзвуковом диффузоре (после прямого скачка на входе, рис. 9) дали скорость воздуха V 2 = 260 м/с и температуру торможения Т 0 = 400 К. Определить коэффициент восстановления полного давления на входе в диффузор.

68. Воздух истекает из сопла при числе М1 = 2,5 под действием давления в форкамере p 01 = 16 атм. Температура в форкамере Т 0 = 288 К. Расширение воздуха расчетное. Определить (рис.10) параметры до и после прямого скачка: p 1, М2, p 2, s, Т 1, Т 2, r1, r2, r01, r02.

69. Определить скорость сверхзвукового потока, текущего при температуре t = -50 °С и давлении p = 1атм, если давление в критической точке трубки Пито равно 12 атм.

70. Трубка полного напора, установленная на самолете, показывает на высоте 15000 м абсолютное давление 71100 Н / м2. Найти скорость полета.

71. Температура торможения, замеренная в полете на высоте 4000 м, оказалась равной t 0 = 107 °С. Определить число Маха М1 и скорость полета V 1, число Маха М2 и скорость воздуха за прямым скачком впереди крыла V 2, значение критической скорости aкр и давление в критической точке крыла p 02.

72.

 
 

Статическое давление за фронтом плоской ударной волны, распространяющейся в неподвижном воздухе на уровне земли, равно 100 атм. Найти температуру воздуха за фронтом волны. Примечание: зависимость теплоемкости воздуха от температуры не учитывать.

73. ЛА движется на высоте Н = 10000 м со скоростью V = 2000 км/ч. Чему равна его скорость относительно частиц воздуха, по которым прошла прямая ударная волна, возникшая перед головной частью корпуса?

74. Самолет летит на высоте Н = 10000 м со скоростью V = 1500 км/ч. Какое абсолютное давление покажет трубка полного напора, установленная на самолете?

75. Термопара в кожухе (рис.7) показала температуру 355 К, температура воздуха в потоке до скачка 260 К. Найти скорость воздуха до и после прямого скачка.

76. Воздух на расчетном режиме истекает из баллона, где он имеет температуру 20 °С, через сопло, имеющее площадь критического сечения F кр = 169 мм2. После прямого скачка скорость потока равна V 2 = 170 м/с. Найти скорость воздуха до скачка и площадь выходного сечения сопла.

77. Подсчитать давление p 02 в камере ВРД самолета, летящего на высоте Н = 10 км со скоростью V = 2160 км/ч, при наличии прямого скачка на входе и давление p 01, которое получилось бы в камере, если бы торможение было изоэнтропическим.

78. Определить энтальпию i 0 сверхзвукового потока, текущего при температуре t =-50°С, если за прямым скачком уплотнения число Маха М2 = 0,52.

 

 

3.2. Косые скачки уплотнения назад

79. В струе воздуха со скоростью V 1 = 700 м/с, истекающей из баллона, где температура Т 0 = 288 К, возник плоский скачок уплотнения, фронт которого наклонен под углом b = 50° к направлению скорости воздуха до скачка. Найти V 2 - величину скорости потока после скачка и Q - угол отклонения потока в скачке.

80. Поток воздуха, имеющий скорость V 1 = 530 м/с и М1 = 2, обтекает внутренний тупой угол, поворачиваясь при этом на 20°. Определить скорость потока V 2 после скачка.

81. Полуугол раствора клина Q = 22°. Теневой фотоснимок показывает, что угол наклона косого скачка на носике клина к скорости невозмущенного потока b = 64°. Найти соотношение плотностей воздуха до и после скачка уплотнения.

82. Определить угол наклона присоединенного скачка уплотнения b и отношение скоростей V 2 / V 1 за и перед косым скачком в плоском сверхзвуковом потоке (k =1,2), если заданы отношение плотностей и угол наклона преграды Q = 30°.

83. Найти угол наклона присоединенного скачка уплотнения b и отношение скоростей V 2 / V 1 за и перед косым скачком в плоском сверхзвуковом потоке (k =1,1), если заданы отношение плотностей и угол наклона преграды Q = 35°.

84. Разность давлений Па, отношение плотностей , а плотность = 1,226 кг/м3. Определить разность энтальпий (i 2 - i 1) на косом скачке уплотнения.

85. Разность давлений Па, отношение плотностей , а плотность = 14,88 кг/м3. Определить разность энтальпий (i 2 - i 1).

86. Определить коэффициент давления за скачком уплотнения при условии, что угол его наклона b = 30°, а перед скачком число М1 = 5. Сравнить два значения коэффициента для k = 1,2 и для k = 1,4.

87. Рассчитайте параметры воздуха () за косым скачком уплотнения и угол наклона скачка для следующих условий: число М1 = 11, угол поворота потока за скачком Q = 40°, высота полета Н = 5 км.

88. Известны угол наклона косого скачка уплотнения b = 55°, угол поворота за этим скачком Q = 41°, а также высота полета Н = 10 км. Определить число М1 перед скачком, а также соответствующие параметры непосредственно за ним ().

 

 

назад

Дата добавления: 2015-08-02; просмотров: 751 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
ДВУМЕРНЫЕ ИЗОЭНТРОПИЧЕСКИЕ СВЕРХЗВУКОВЫЕ ТЕЧЕНИЯ ГАЗА| БОЛЬШИЕ СВЕРХЗВУКОВЫЕ СКОРОСТИ. ПОГРАНИЧНЫЙ СЛОЙ В НЕСЖИМАЕМОМ ГАЗЕ
mybiblioteka.su - 2015-2024 год. (0.01 сек.)