Разбор задач.

1. Рассмотрим игру, в которой игрок располагает двумя стратегиями, а игрок - тремя. Пусть матрица выигрышей имеет следующий вид:

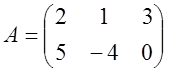
Проанализировав свои возможные выигрыши, игрок останавливается на первой стратегии, которая обеспечивает ему максимальный гарантированный выигрыш, равный 1. Точно так же игрок выбирает минимальное значение из возможных максимальных проигрышей, равное 1:

Следовательно, в этой игре существуют совместимые выборы, т.е. . Такая игра называется вполне определенной или игрой, имеющей решение в чистых стратегиях.

2. Рассмотрим платежную матрицу размера :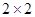

.

Поскольку 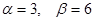, и , то игроки будут максимизировать свой выигрыш путем применений своих смешанных стратегий. Игрок в течение игры с вероятностью 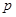будет выбирать свою первую стратегию, и с вероятностью - вторую. Поэтому вектор смешанных стратегий для первого игрока будет равен 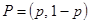, для игрока он будет задаваться как .

Выпишем уравнения математического ожидания выигрыша игрока . В случае, когда игрок применяет смешанную стратегию, а игрок - чистые стратегии. Тогда:

Выпишем теперь уравнения математического ожидания выигрыша игрока , в случае, когда он применяет свои смешанные стратегии, а игрок - чистые:

В результате решения двух систем мы получим значения вероятностей, с которыми игроки будут применять ту или иную стратегию на протяжении партии. Они будут равны , , при этом цена игры

Основная теорема теории игр гарантирует, что в рассматриваемой ситуации существует «устойчивая» пара стратегий, для которых минимальный проигрыш одного игрока совпадает с максимальным выигрышем другого. Устойчивость стратегий означает, что каждый из игроков, отклоняясь от оптимальной стратегии, лишь ухудшает свои шансы.

3. Решить игру:

.

Решение:

Так как , и , то игра седловой точки не имеет (заметим, что исследование наличия седловой точки у игры нужно обязательно проводить).

Выпишем уравнения для математического ожидания выигрыша:

Изобразим указанные прямы на плоскости:

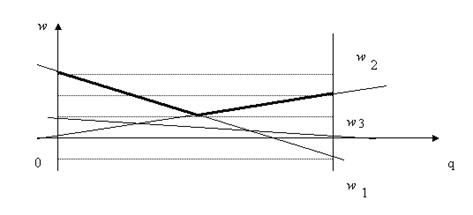
Игрок следует своей максминной стратегии. Координаты искомой точки будут находиться на пересечении первой и второй прямой:

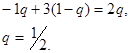
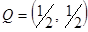Следовательно, вектор оптимальных смешанных стратегий для игрока равен: и .

Для нахождения составим систему уравнений:

Решая систему, находим .

Ответ: 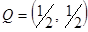, и .

4. Решить игру с матрицей:




1. В соответствии с алгоритмом определим, существуют ли в ней доминируемые стратегии, чтобы исключить их. Доминируемых стратегий нет. 


2. Поскольку матрица содержит отрицательные числа, то нужно добиться, чтобы все её элементы были неотрицательны, прибавив ко всем её элементам число, равное модулю наименьшего числа матрицы. Минимальный элемент матрицы равен - 0,1, его модуль равен 0,1. Прибавим ко всем элементам платёжной матрицы число, равное 0,1, в результате получим:


 


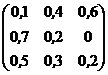
Умножим все элементы полученной матрицы на 10, чтобы удобнее проводить последующие вычисления. 





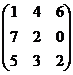
Проведённые аффинные преобразования на оптимальных стратегиях не скажутся, а цену игры мы восстановим, сделав обратные преобразования (разделим полученную сумму на 10 и отнимем 0,1). 
Припишем строкам вероятности p₁, p₂, p₃.


 


Тогда среднее значение (математическое ожидание) выигрыша игрока A при применении игроком B своей первой стратегии равен 1·p₁ + 7·p₂ + 5·p₃ (первый столбец поэлементно умножаем на вероятности p₁, p₂, p₃ и полученные произведения суммируем). Это выигрыш не может быть меньше гарантированной цены игры V: 1·p₁ + 7·p₂ + 5·p₃ ≥ V. Аналогично для других стратегий игрока B. 





Разделим обе части неравенства на V и введём обозначения y_i = p_i/V (i = 1, 2, 3.): 



 


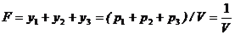
Игрок A стремиться повысить цену игры (V→ max). Поэтому F → min. 
 Получили задачу линейного программирования: 


F = y₁ + y₂ + y₃ → min


 


Аналогично припишем столбцам вероятности q₁, q₂, q₃.


 


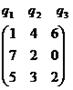
Тогда средний проигрыш игрока B при применении игроком A его первой стратегии равен 1·q₁ + 4·q₂ + 6·q₃ (1-ю строку поэлементно умножаем на вероятности q₁,q₂, q₃ и полученные произведения суммируем). Этот проигрыш не может быть больше цены игры V: 1·q₁ + 4·q₂ + 6·q₃ ≤ V. Аналогично для других стратегий игрока A.


 


Разделим обе части неравенств на V и введём обозначения x_i = q_i /V (i = 1, 2, 3)





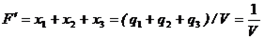
Игрок B стремится понизить цену игры (V→min), поэтому F^/ → max. 
Получили задачу линейного программирования:


F' = x₁ + x₂ + x₃ → max




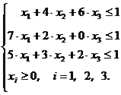
Полученные задачи являются взаимно двойственными задачами линейного программирования. Решим любую из них симплекс-методом. Итак, оптимальные стратегии: 
Р^*=(3/8; 0; 5/8), Q^*=(1/2; 0; 1/2), 
цена игры: 
для модифицированной задачи V= 3,5, 
а для исходной задачи V^/ = 3,5/10-0,1 = 0,25.

Дата добавления: 2015-08-02