Прямая на плоскости

Контрольная работа № 2

Аналитическая геометрия и векторная алгебра (теория)

Прямая на плоскости

1. Расстояние d между двумя точками А(x₁;у₁) и В(х₂;y₂) определяется по формуле:

a)

b)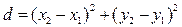

c)

d)

2. Уравнение прямой с угловым коэффициентом имеет вид

a) y = kx +b

b) Ax +Ву +С = 0

c)

d) у – у₀ = k₀ (х – k₀)

e)

3. Уравнение прямой в общем виде имеет вид:

a) y = kx +b

b) Ax +Ву +С = 0

c)

d) у – у₀ = k₀ (х – k₀)

e)

4. Уравнение прямой в отрезках имеет вид:

a) y = kx +b

b) Ax +Ву +С = 0

c)

d) у – у₀ = k₀ (х – k₀)

e)

5. Уравнение прямой, проходящей через данную точку М(х₀;у₀), и имеющей данный угловой коэффициент k = k₀ имеет вид:

a) y = kx +b

b) Ax +Ву +С = 0

c)

d) у – у₀ = k₀ (х – х₀)

e)

6. Уравнение прямой, проходящей через две данные точки А(х_А;у_А) и В(х_В;у_В), имеет вид

a) y = kx +b

b) Ax +Ву +С = 0

c)

d) у – у₀ = k₀ (х – х₀)

e)

7. Каноническое уравнение прямой имеет вид

a) y = kx +b

b) Ax +Ву +С = 0

c)

d)

e)

8. Параметрические уравнения прямой имеет вид

a)

b) Ax +Ву +С = 0

c)

d)

e)

9. Расстояние от точки М(х₀;у₀) до прямой Аx +Вy +С = 0 можно найти по формуле

a)

b)

c)

10. Пусть даны две прямые: L₁: y = k₁ x +b₁, где k₁ = tg α, L₂: y = k₂ x +b_2, где k₂ = tg β.

Тогда k₁ = k₂ –это условие ……….. двух прямых.

a) параллельности

b) перпендикулярности

c) пересечения

d) совпадения

11. Пусть даны две прямые: L₁: y = k₁ x +b₁, где k₁ = tg α, L₂: y = k₂ x +b₂, где k₂ = tg β.

Тогда k₁k₂ = -1 - это Условие …… двух прямых.

a) параллельности

b) перпендикулярности

c) пересечения

d) совпадения

12. Если в общем уравнении прямой Ах+Ву+С=0, коэффициент С=0, а ,то

a) прямая проходит через начало координат

b) прямая параллельна оси Ох

c) прямая параллельна оси Оу

d) прямая совпадает с осью Оу

e) прямая совпадает с осью Ох

13. Если в общем уравнении прямой Ах+Ву+С=0, коэффициент А=0, а ,то

a) прямая проходит через начало координат

b) прямая параллельна оси Ох

c) прямая параллельна оси Оу

d) прямая совпадает с осью Оу

e) прямая совпадает с осью Ох

14. Если в общем уравнении прямой Ах+Ву+С=0, коэффициент В=0, а 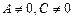,то

a) прямая проходит через начало координат

b) прямая параллельна оси Ох

c) прямая параллельна оси Оу

d) прямая совпадает с осью Оу

e) прямая совпадает с осью Ох

15. Если в общем уравнении прямой Ах+Ву+С=0, коэффициент В=С=0, а 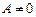,то

a) прямая проходит через начало координат

b) прямая параллельна оси Ох

c) прямая параллельна оси Оу

d) прямая совпадает с осью Оу

e) прямая совпадает с осью Ох

16. Если в общем уравнении прямой Ах+Ву+С=0, коэффициент А=С=0, а ,то

a) прямая проходит через начало координат

b) прямая параллельна оси Ох

c) прямая параллельна оси Оу

d) прямая совпадает с осью Оу

e) прямая совпадает с осью Ох

17. Вектор {A,B} по отношению к прямой Ах+Ву+С=0

a) перпендикулярен, и называется нормальны м вектором прямой

b) параллелен, и называется нормальным вектором прямой

c) перпендикулярен, и называется направляющим вектором прямой

d) параллелен, и называется направляющим вектором прямой

e) пересекает прямую

18. Вектор {-В, А} по отношению к прямой Ах+Ву+С=0

a) перпендикулярен, и называется нормальны м вектором прямой

b) параллелен, и называется нормальным вектором прямой

c) перпендикулярен, и называется направляющим вектором прямой

d) параллелен, и называется направляющим вектором прямой

e) пересекает прямую

19. В уравнении прямой, заданном в виде у=kx+b, коэффициент k называется

a) угловым коэффициентом прямой

b) отрезком, который отсекает прямая на оси Оу

c) отрезком, который отсекает прямая на оси Ох

d) расстоянием от начала координат до прямой

20. В уравнении прямой, заданном в виде у=kx+b, коэффициент b называется

a) угловым коэффициентом прямой

b) отрезком, который отсекает прямая на оси Оу

c) отрезком, который отсекает прямая на оси Ох

d) расстоянием от начала координат до прямой

21. В уравнении прямой, заданном в виде , длины отрезков, которые отсекает прямая на осях координат, это

a) числа p и q

b) числа х и у

c) произведение p q

d) сумма p + q

22. Установите соответствие

1) Уравнение прямой на плоскости с угловым коэффициентом

2) Уравнение прямой на плоскости, проходящей через две заданные точки

3) Уравнение прямой на плоскости в отрезках

4) Общее уравнение прямой на плоскости

a)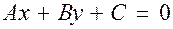

b)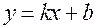

c)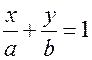

d)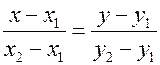

23. Установите соответствие

1) Нормальное уравнение прямой на плоскости

2) Уравнение прямой на плоскости, проходящей через данную точку в данномнаправлении

3) Уравнение прямой на плоскости с угловым коэффициентом

4) Уравнение прямой на плоскости в отрезках

a)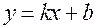

b)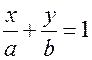

c)

d)

24. Установите соответствие

1) Нормальное уравнение прямой на плоскости

2) Общее уравнение прямой на плоскости

3) Уравнение прямой на плоскости, проходящей через две заданные точки

4) Уравнение прямой на плоскости в отрезках

a)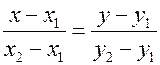

b)

c)

d)

25. Две прямые заданы общими уравнениями вида: Ах+Ву+С=0,тогда

1) прямые пересекаются (не перпендикулярны),если

2) прямые совпадают, если

3) прямые параллельны, но не совпадают, если

4) прямые перпендикулярны, если

a)

b)

c)

d)

26. Угол между прямыми на плоскости вычисляется по формуле:

a)

b)

c)

d)

---

Дата добавления: 2015-08-02