Количественная оценка технического состояния зажимов контактной сети по падению напряжения на зажимах

2.1. Уравнение линейной регрессии:

(2.1)

где - коэффициент корреляции между и ;

- среднее значение времени безотказной работы;

- среднее значение падения напряжения на зажиме;

- среднеквадратическое отклонение падения напряжения ;

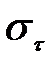- среднеквадратическое отклонение времени безотказной работы.

2.2. Среднее значение падения напряжения на зажиме определяется по следующей формуле:

(2.2)

2.3. Среднее значение времени безотказной работы определим по формуле:

(2.3)

2.4. Падение напряжения определим по формуле:

; (2.4)

где U₃₁-первое значение выборки падения напряжения на зажиме;

- среднее значение падения напряжения на зажиме.

2.5. Время безотказной работы определим по формуле:

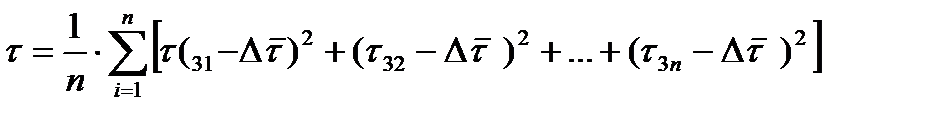; (2.5)

где ₃₁-первое значение выборки времени безотказной работы.

-среднее значение времени безотказной работы.

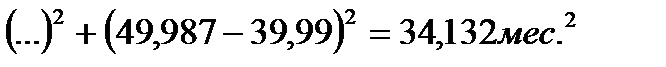
2.6. Среднеквадратическое отклонение падения напряжения:

= ; (2.6)

где Д(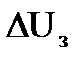) – дисперсия падения напряжения.

, мес., (2.7)

где Д(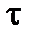) – дисперсия времени безотказной работы.

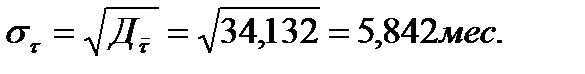
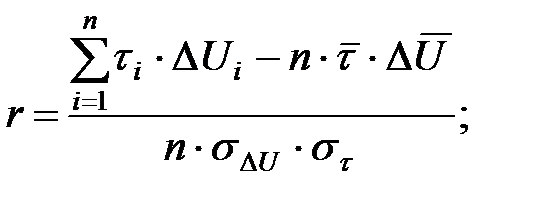(2.8)

где - выборка времени безотказной работы;

- выборка падений напряжения;

- среднее значение времени безотказной работы;

- среднее значение падения напряжения на зажиме;

- среднеквадратическое отклонение падения напряжения ;

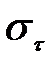- среднеквадратическое отклонение времени безотказной работы.

Таким образом, уравнение линейной регрессии примет вид:

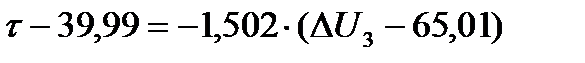
Дата добавления: 2015-08-02