Приклад оптимізації рангу живучості трьох етапної системи з одномірним зв’язком

Розглянемо простий приклад оптимізації рангу живучості трьохетапної системи з одномірним зв’язком типу «один ресурс-один продукт» на кожному з етапів. Випускаючим в цій системі є третій етап.

Нехай вихідний стан по запасах і коефіцієнтах жорсткості зв’язку «вхід-вихід» по кожному з етапів буде наступним:

Технологічний етап (і)
Запас (ri)
Коефіцієнт жорсткості (gi)	1,05	1,1	1,2

Згідно (1.10) повний резерв , де 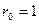, , – коефіцієнти еластичності етапів системи.

З вищенаведених даних і формули (1.10) випливає, що система має ранг живучості 1 при розмірі збурення (недопоставки) 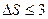, ранг живучості 2 при і ранг живучості 3 при .

Компенсувати недопоставку можна по-різному варіюючи використанням запасів кожного етапу. Так, недопоставку можна погасити на першому етапі , проте можна взагалі не гасити, тоді на другому етапі почнеться обурення – недопоставка 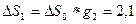. Її можна погасити на другому етапі цілком () чи відправити на третій етап в об’ємі 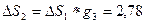. Між цими варіантами можливі і проміжні.. Оптимальний варіант буде відповідати мінімуму затрат на використання запасів на всіх етапах.

Даний приклад допускає і таку інтерпретацію: розглядається стратегія погашення боргу (кредиту) протягом трьох років. Коефіцієнти жорсткості – що прогресує в часі () процент за відтермінування боргу. Резерв – дохід, що планується на відповідний рік, який може бути направлений в сферу виробництва для отримання додаткового економічного ефекту.

Нехай функція інтегрального ефекту за три роки має вигляд:

Де – об’єм погашення боргу (використання запасу) в році i; коефіцієнти 1;0,8;0,6 характеризують дисконтовані вклади коштів виробництво в першому, другому і третьому роках відповідно. При стратегії погашення боргу його залишок буде становити:

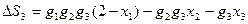
Вимоги повного погашення (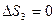) рівносильні пошуку таких, що

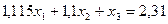
Максимізуючи F при таких обмеженнях, легко провірити, що оптимальною буде стратегія (тобто борг найкраще погасити на третьому році, враховуючи проценти). Ефект при цьому складає .

Таким чином, при даних умовах, оптимальний ранг живучості може бути вибраний таким, що = 3.

У випадку можливості управління коефіцієнтами жорсткості також можлива і постановка відповідних оптимізаційних задач.

Якщо елементи класу обурень є випадковими величинами, то про можливості компенсації цих обурень, тобто живучості системи, можна говорити тільки у ймовірносно му сенсі. Однак, випадковим може виявитись ранг живучості. Можна в цьому випадку говорити про закон ймовірності розподілу рангу живучості як випадкової величини. Можна вимагати, щоб мовірність того чи іншого рангу живучості була не нижче заданої норми (границя надійності рангу живучості). В такому випадку проявляється зв'язок живучості з надійністю.

Для ілюстрації сказаного в умовах попереднього прикладу припустимо, що – це випадкова величина з математичним очікуванням . Таким чином клас обурю вальних впливів – це безліч ймовірних реалізацій з середнім (по ймовірності) значенням .

Будемо вважати, що обурення компенсовано, якщо при плановому випуску і ймовірності G того, що це завдання буде виконано при тій чи іншій недопоставці ресурсу.

Тоді скориставшись оцінкою надійності H, отримаємо, що

Ця оцінка може бути незадовільною. Її можна підвищити різними шляхами, зокрема, за рахунок зниження . Неважко підрахувати, що при переході до , об’єм поставки ресурсів, що вимагається є менше 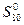на 7,212, а . При переході до надійність і т.д.

Перехід до нижчих значень, підвищує оцінку надійності живучості системи, і кінцевим результатом виступає відмова від частини продукції. Наприклад, при переході від до система підвищує оцінку надійності живучості на величину , а «недоотримання» продукції .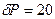

Аналогічно можна прослідкувати залежність підвищення рангу живучості при зниженні цільового завдання .

В сучасних умовах, зокрема, об’єм може (повинен) бути вибраним з врахуванням того, що фактичний об’єм 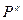(сирос) являється випадковою велечиною. В такій ситуації вибір рівня зумовить ймовірнісну оцінку живучості системи. Якщо оцінка виявиться низькою, то може бути рекомендовано зниження для підвищення гарантії кінцевих результатів, зниження ризику і виплати неустойок.

Поряд з варіацією параметра управління живучістю здійснюється і іншими факторами, наприклад, уточненням інформації про параметри системи (поставки ресурсів, норми затрат, попит і т.д.). процес такого управління потребує відповідних затрат, зв’язаних з проведенням додаткових досліджень: від голого-розвідних до широкомасштабного маркетингового. Проте в результаті уточнення інформації підвищується живучість і надійність багато етапних виробничих систем.

Приведений вище приклад мав найпростішу структуру трьох етапного процесу припускаючи, припускаючи, що на кожному етапі існує всього лише один об’єкт, хоча в реальності це не так. Проте багато положень, висказаних вище з приводу живучості, можуть бути перенесені на більш складні структури технологічних зв’язків.

Можливо розгляд задач живучості по відношенню до такого виду обурень, як додаткове завдання по випуску продукції системи (чи підвищенню інших економічних показників). Таке завдання можливо компенсувати різними шляхами, наприклад запасами готової продукції. Проте утримання таких запасів може бути дорогим. Якщо час на задоволення не лімітовано, то можна виробити з первинних ресурсів, тобто використовуючи запаси і резерви перших технологічних етапів. Такі запаси можна назвати некваліфікованими на відмінну від запасів-напівфабрикатів.

Кваліфікацію запасів можна оцінювати числом технологічних етапів, результатом яких вони являються. При інших рівних умовах більш кваліфіковані запаси дорожчі, але зато вони володіють більш високою маневреністю, тобто швидше перетворюються в готовий продукт.

Якщо зв'язок «ресурс S – продукт P» (вектор) задається перехідною матрицею (матриця еластичності), то для задоволення необхідний запас ресурсу . В цьому випадку запас готової продукції в об’ємі еквівалентний запасу вихідних ресурсів в об’ємі , якщо час на перетворення в не лімітовано. Проте в випадку лімітованого терміну запас може виявитись нееквівалентним . В цьому випадку в багато етапних системах можлива організація набору кваліфікованих запасів. Серед множини всіх таких наборів можна вказати оптимальний з позиції будь-якого критерія і в такому випадку говорити про оптимальну кваліфіковану структуру запасів.

В постановці таких задач необхідно враховувати темпові характеристики технологічних переділів.

Нехай виробнича система складається з N технологічних етапів; кожний етап і має свою перехідну матрицю , що зв’язує вектор вхідних і вихідних параметрів відношенням ; і нехай на вихід останнього N -го етапу поступило обурення – необхідність в додатковому об’ємі випуску продукції.

Якщо на проміжних етапах нема запасів, то для компенсації необхідно використати запас первинного ресурсу .

Проте його проходження по всьому технологічному ланцюгу для перетворення в потребує відповідного часу, який може бути більшим встановленого споживачами терміну для реалізації . Цей термін може бути вибраний як оптимальний в результаті договірних відносин між виробником і споживачем продукції. Вкластися в термін дозволяє система резервів, зокрема запасів. Нехай – вектор запасів і- го етапу, який ми шукатимемо. Тоді умова компенсації з допомогою запасів за N етапів означає, що виконується векторне відношення

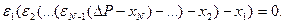
Представимо для простоти, що технологічний процес неперервний, тобто з етапу на етап передається для переробки як завгодно малий об’єм напівфабрикату. Крім того, якщо час на транспортування між етапами рівний нулю, а час 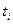на переробку і- им етапом вектора напівфабриката, що являється функцією від цього вектора, може бути конструктивно розраховано, то обмеження по часу на компенсацію при заданих може бути записано як

В якості критерію може бути взятий мінімум затрат на утримання запасів

Де 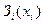– функція затрат на організацію та утримання запасу і -им етапом.

Можливий і критерій мінімізації t, тобто постановка задачі на швидкодію (в термінах оптимального управління) по погашенню обурення при обмеженнях на організацію і утримання запасів;

Де З – виділений фонд на утримання запасів.

Можливі і інші постановки, що модифікують вид функцій і умов. Зокрема, можлива постановка задач з врахуванням потреб надійності погашення випадкової величини , досягнення терміну компенсації . Це можна зробити наступним чином. Нехай як випадкова величина може приймати значення з ймовірностями відповідно Припустимо, що початкове планове значення характеризується вектором . Позначимо через вектор неповної компенсації . Тоді умову можна записати у вигляді:

Обмеження по надійності випуску

Де – вектор нормативної надійності по кожному продукту. Його можна розглядати як надійне обмеження живучості системи.

Час компенсації в цих умовах стає функцією від , тобто . Можна також записати надійне обмеження на час компенсації з класу , наприклад, у вигляді:

Де – нормативний час виконання любого додаткового завдання з класу обурень, що розглядається.

В деяких випадках різноманітність виробничих елементів, продукції, що виробляється, ресурсів, що використовується і тому подібне дозволяє найкращим способом вирішити задачу створення необхідних резервів без збитків для досягнення кінцевих цілей.

В загальному випадку вектор може містити і негативні компоненти (падіння попиту на відповідні продукти). В ці моменти також можливе створення і поповнення запасів під їх оптимальну кваліфікаційну структуру.

Дата добавления: 2015-08-02