Примеры. Пример 23. Определить крутящие моменты в сечениях вала, расчетная схема которого

Пример 23. Определить крутящие моменты в сечениях вала, расчетная схема которого показана на рис. 2.5,а. Вращающие моменты равны:

Н×м.

Рис. 2.5. К примеру 23

Решение. Для выявления моментов внутренних сил в сечениях вала мысленно отбросим одну часть вала (например, правую часть от сечения I-I) и рассмотрим равновесие оставшейся части (рис. 2.5, б). Эта часть вала свободна от действия вращающих моментов, и поэтому в рассматриваемом сечении I-I не будет возникать крутящий момент T_ZΙ = 0.

Аналогично поступим для определения крутящего момента в сечении II-II. Рассматриваемая часть вала находится в равновесии (сумма моментов равна нулю), следовательно,

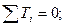
Отсюда

Н×м.

В сечении III-III крутящий момент равен нулю (T_ZIII = 0), так как в правой части вала от этого сечения не приложены моменты внешних сил (рис. 2.5, г).

При решении задач методом сечения удобнее отбрасывать ту часть тела, в которой приложено больше внешних сил.

Ответ: 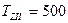Н×м;

Пример 24. Определить опорные реакции балки (рис.2.6,a), концы которой шарнирно закреплены. Балка нагружена парой сил с моменто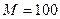м кН×м.

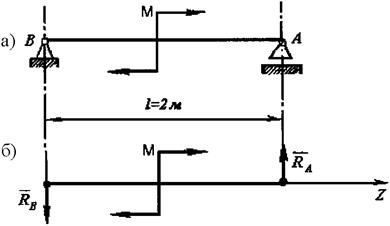
Рис.2.6. К примеру 24

Решение. Прежде всего необходимо наметить направление реакций опор (рис. 2.6, б). Так как к балке приложена пара сил, то и уравновесить ее можно только парой сил. Следовательно, реакции опор равны между собой по величине, параллельны, но противоположно направлены. Заменим действие опор их реакциями. Правая опора А - плоскость, следовательно, направление опорной реакции R_A перпендикулярно этой плоскости, а опорная реакция R_B ей параллельна и противоположно направлена. Балка находится в равновесии, поэтому сумма моментов пар сил, приложенных к ней, равна нулю:

,

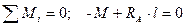откуда

кН.

Ответ: 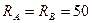кН.

Пример 25. Брус АВ с левой шарнирно-подвижной опорой и правой шарнирно-неподвижной нагружен тремя парами (рис. 2.7), моменты которых 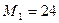кН×м, кН×м, кН×м. Определить реакции опор.

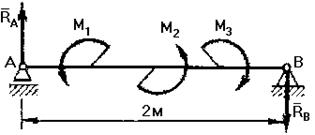
Рис. 2.7. К примеру 25

Дата добавления: 2015-08-02