Читайте также:
|
Применим закон Ома для неоднородного участка цепи: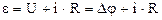 
, где 
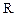- сопротивление элементов контура.
В колебательном контуре: 
; 
= 
- разность потенциалов на обкладках конденсатора. Подставив в исходное уравнение, получим: 
. Поскольку сила тока 
= 
, а 
= 
, то уравнение примет вид: 
.
Это - дифференциальное уравнение второго порядка. Если активное сопротивление 
, уравнение перепишется: 
.
Решением такого уравнения является функция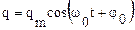 
, где 
- фазовый угол (или фаза колебаний), который выражается в радианах, 
- начальная фаза колебаний (при t=0), 
- собственная круговая частота колебаний в контуре. Сила тока в колебательном контуре: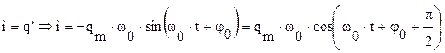 
Напряжение в контуре: 
.
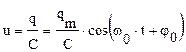В математике и физике колебания, которые подчиняются синусоидальному или косинусоидальному закону, называются гармоническими.
 |
В гармонических колебаниях максимальное значение функции называют амплитудой. Значение функции становится максимальным, если величины cos или sin становятся равными 1. Таким образом, амплитуда колебаний силы тока в контуре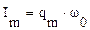 
, а амплитуда колебаний напряжения на конденсаторе 
.
При начальной фазе 
можно получить закон колебаний силы тока и напряжения в колебательном контуре:
; 
.
Отсюда следует, что в колебательном контуре фаза колебаний силы тока в катушке отстает от фазы колебания напряжения на конденсаторе на угол 
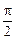(рисунок 39).
 |
Время, затраченное на одно полное колебание, называется периодом колебаний Т (рисунок 39).
|
. 
. Размерность частоты:
|
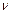]=1 Гц (герц).
Один герц – это частота, при которой одно полное колебание происходит за одну секунду.
Если ток изменяется по закону: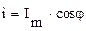 
, где фаза 
. Угловая частота 
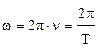, поэтому ток в любой момент времени 
может быть вычислен по формулам:
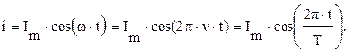
Аналогично напряжение:
Период собственных колебаний контура 
определяется формулой Томпсона: 
.
Отсюда: 
– собственная частота колебаний в контуре и 
.
Из этих формул следует, что при достаточно малых значениях L и C в контуре можно получить электромагнитные колебания высокой частоты, измеряемые миллионами герц и больше.
В реальном электрическом контуре из-за потерь энергии на нагревание проводников и диэлектриков энергия магнитного и электрического полей постепенно превращается во внутреннюю энергию и колебания через некоторое время прекращаются. Такие колебания называются затухающими.
При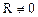 
период колебаний 
Дата добавления: 2015-08-02; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Превращение энергии в колебательном контуре | | | Вынужденные электрические колебания. Переменный ток. Генератор переменного тока. Мгновенное, амплитудное и действующее значения Э.Д.С., напряжения и силы тока |
