Расчет однородной неразветвленной магнитной цепи

Прямая задача расчета однородной магнитной цепи (рис. 8.7) выполняется в следующей последовательности.

1. По заданному магнитному потоку Ф и габаритам магнитопровода цепи определяется магнитная индукция , где - площадь сечения магнитопровода, которая по всей длине l имеет одинаковое значение.

Рис. 8.7

Рис. 8.8

2. По кривой намагничивания для заданного материала сердеч­ника по вычислен­ной индукции определяется напряженность магнитного поля магнитной цепи Н.

3. По закону полного тока определяется магнитодвижущая сила обмотки, расположенной на магнитопроводе, по выраже­нию , где l - длина средней линии сердечника, кото­рая определяется по заданным габаритам.

Обратная задача расчета однородной магнитной цепи (рис. 8.8) решается в следующей последовательности.

1. По заданной магнитодвижущей силе и габаритам магнитопровода магнитной цепи определяется напряженность маг­нитного поля цепи 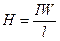, где l - длина средней линии магни­топровода, .

2. По вычисленной напряженности по кривой намагничивания для заданного ферро­магнитного материала сердечника магнитной цепи определяется индукция В магнитного поля однородной цепи.

3. Определяется искомый магнитный поток цепи , где S - площадь сечения магнитопровода магнитной цепи, .

При расчете неразветвленной однородной магнитной цепи может быть предусмотрено определение других параметров магнитной цепи, например магнитной проницаемости материала сердечника в заданном режиме работы. Для этого применяется выражение .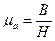

Неразветвленная магнитная цепь с постоянным магнитом

Рассмотрим расчет простейшей неразветвленной магнитной цепи с постоянным магнитом. Предположим, что тороид длиной l и пло­щадью поперечного сечения S (рис. 6.13, а) изготовлен из магнитно-твердого материала, часть предельного статического цикла гистере­зиса которого В (Н) изображена на рис. 6.13, б. Материал тороида был предварительно намагничен так, что его магнитное состояние ха­рактеризуется остаточной индукцией В_r.

Вырежем из тороида участок длиной l_в << l (рис. 6.13, в). Остав­шаяся часть тороида будет постоянным магнитом, а в образовавшемся воздушном зазоре магнитное поле возбуждается этим постоянным магнитом. Пренебрегая неоднородностью магнитного поля в воздушном зазоре, будем считать, что всюду в зазоре магнитное поле харак­теризуется напряженностью магнитного поля H_в, и индукцией В_в=m_o*H_в. Учтем, что вследствие «выпучивания» магнитных линий в воз­душном зазоре площадь поперечного сечения воздушного зазора S_в больше площади поперечного сечения постоянного магнита S_м = S.

По закону полного тока для контура, совпадающего со средней линией магнитопровода,

(6.8)

где Н_м и l_м - напряженность магнитного поля и длина средней линии постоянного магнита. Из (6.8) следует, что

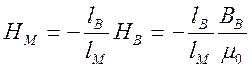(6.9)

Кроме того, так как магнитный поток Ф в неразветвленной магнитной цепи постоянен, то

(6.10)

Подставив значение индукции в воздушном зазоре В, из (6.10) в (6.9), получим уравнение прямой линии, проходящей через начало координат (рис. 6.13, б):

(6.11)

где - коэффициент размагничивания постоянного магнита.

Точка пересечения прямой Н_м = - N_мВ_м и предельного статиче­ского цикла гистерезиса материала В (Н) определяет индукцию в маг­ните , а следовательно, и индукцию в воздушном зазоре (6.10).

Если в воздушный зазор медленно вводить ферромагнитный замыкатель с малым магнитным сопротивлением, то значение индукции в магнитопроводе будет увеличиваться по частному гистерезисному циклу, показанному на рис. 6.13, б пунктиром. При многократном магнитном замыкании и размыкании воздушного зазора изменение индукции магнита происходит по некоторому установившемуся част­ному циклу.

Для получения больших значений индукции в воздушном зазоре необходимо изготавливать постоянный магнит из магнитно-твёрдых. материалов, т. е. с большим значением коэрцитивной силы Н_с.

Дата добавления: 2015-08-02