Магнитная проницаемость

Магнитная индукция в магнитном поле зависит от абсолютной магнитной проницаемости 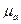, характеризующей магнитные свойства среды, в которой создается поле.

Абсолютная магнитная проницаемость среды характеризует способность среды намагничиваться. Единицей измерения является:

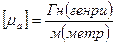(3)

Абсолютная магнитная проницаемость вакуума 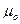- величина постоянная и называется магнитная постоянная. Ее значение равно

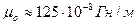
Абсолютную магнитную проницаемость любой среды 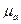удобно выражать через магнитную постоянную 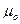и магнитную проницаемость 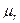, которая показывает, во сколько раз абсолютная магнитная проницаемость среды больше или меньше магнитной проницаемости

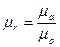
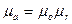
Иногда 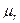называют относительной магнитной проницаемостью.

В зависимости от магнитной проницаемости все вещества делятся на диамагнитные, парамагнитные и ферромагнитные.

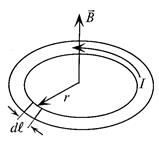
Рис. 7.3.

7.4. Магнитный поток

Магнитный поток Ф сквозь площадку S, перпендикулярную вектору магнитной индукции В_H в однородном магнитном поле, определяется выражением

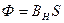(7.6)

Магнитный поток измеряется в веберах (основная единица):

[ Ф ] = [ ВS ] = 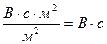= Вб (вебер).

В практических расчетах встречается единица магнитного пото­ка максвелл, которая в 10⁸ раз меньше вебера: т. е. 1 Мкс = 10^-8 Вб.

Если вектор магнитной индукции В составляет угол β с перпендикуляром к площадке S (рис. 7.4), то нормаль­ная (перпендикулярная) составляющая вектора магнитной индукции В_H опре­деляется как .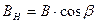

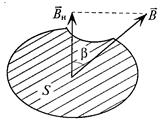
Рис. 7.4

В общем случае при определении магнитного потока через произвольную поверхность в неоднородном магнитном поле площадку S разбивают на бесконечно малые площадки dS, для каждой из ко­торых поле можно считать однородным. Тогда элементарный магнитный поток dФ через элементарную площадку dS определя­ется так:

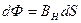
Магнитный поток Ф через всю поверхность площадью S опре­деляется суммированием (интегрированием) элементарных маг­нитных потоков dФ по всей площади S

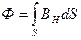
Магнитный поток сквозь замкнутую поверхность равен нулю 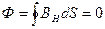, так как каждая магнитная линия, входящая в замкнутую поверхность, должна из нее выйти.

Магнитный поток, как один из параметров магнитного поля, необходимо знать или определять при анализе и расчете режима работы различных электротехнических приборов, устройств и установок (магнитных цепей, электрических машин, трансфор­маторов, электромагнитов различного назначения, электроизме­рительных приборов и др.).

7.5. Напряженность магнитного поля

Напряженность в каждой точке магнитного поля - это расчет­ная величина, характеризующая интенсивность магнитного поля в этой точке, созданного током, без учета среды, в которой создает­ся поле.

Обозначается напряженность магнитного поля буквой Н.

Если в катушку, по которой проходит ток I, внести сердечник из ферромагнитного материала (рис. 7.1г), то величина магнитной индукции В в каждой точке магнитного поля увеличивается, а на­пряженность Н в этих точках остается неизменной.

Разница между напряженностью Н и индукцией В в какой-либо точке магнитного поля (хотя обе величины характеризуют интен­сивность магнитного поля) заключается в том, что напряжен­ность в точке магнитного поля характеризует интенсивность поля в этой точке, созданного током без учета магнитной проницаемо­сти среды, в которой создается поле, а индукция в этой точке ха­рактеризует интенсивность магнитного поля, созданного током и средой, которая намагничивается и изменяет его интенсивность; т. е. напряженность является расчетной величиной, не имеющей физического смысла, так как физически невозможно представить себе, что интенсивность поля не зависит от среды.

Таким образом, соотношение между В и H в какой-либо точке магнитного поля выглядит следующим образом:

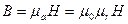(7.7)

т. к. μ_а характеризует способность среды намагничиваться. Следовательно, напряженность в этой точке

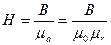(7.8)

Из выражения (7.8) определяем единицу измерения напряжен­ности в любой точке магнитного поля:

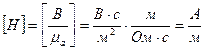
Напряженность - величина векторная, причем направление вектора напряжен­ности в каждой точке совпадает с направ­лением магнитного поля в этой точке (касательная к магнитной линии в этой точке).

Если магнитное поле создано несколь­кими токами, то напряженность в каждой точке этого поля определяется геометри­ческой суммой напряженностей, создан­ных каждым током в этой точке (рис. 7.5).

Очевидно, для каждой точки магнитного поля напряженность имеет определенную величину и направление.

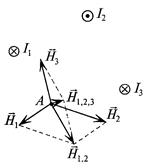
Рис. 7.5

7.6. Закон полного тока

Закон полного тока получен на основании многочисленных опы­тов. Этот закон устанавливает, что интеграл от напряженности магнитного поля по любому контуру (циркуляция вектора напряжен­ности) равен алгебраической сумме тонов, сцепленных с этим контуром:

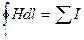(6.1)

причем положительными следует считать те токи, направление кото­рых соответствует обходу контура по направлению движения часо­вой стрелки (правило буравчика). В частности, для контура на рис. 7.6. по закону полного тока

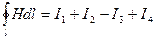
Величина 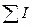в (6.1) называется магнитодвижущей силой (сокра­щенно МДС).

Основной единицей измерения магнитодвижущей силы в системе СИ является ампер (А).

Магнитную цепь большинства электротехнических устройств можно представить состоящей из совокупности участков, в пределах каждого из которых можно считать магнитное поле однородным, т. е. с постоянной напряжен­ностью, равной напряженности магнитного поля H_k, вдоль средней линии участка длиной l_k. Для таких магнитных цепей можно заменить интегрирование в (6.1) суммированием.

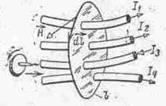
Рис. 7.6.

Если при этом магнитное поле возбуж­дается катушкой с током I, у которой w витков, то для контура магнитной цепи, сцепленного с витками и состоящего из n участков, вместо (6.1) мож­но записать:

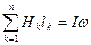(6.2)

Таким образом, согласно закону полного тока МДС F равна сумме произведений напряженностей магнитного поля на длины соответствующих участков для контура магнитной цепи. Произведение 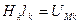часто называют магнитным напряжением участка маг­нитной цепи.

Глава 8 МАГНИТНЫЕ ЦЕПИ И ИХ РАСЧЕТ

8.1. Магнитная цепь

В состав многих электротехнических устройств входят магнитные цепи.

Магнитная цепь представляет собой сочетание тел преимущест­венно из ферромагнитных материалов, в которых замыкается маг­нитный поток.

Простейшей магнитной цепью является сердечник кольцевой катушки, в котором замыкается магнитный поток, со­зданный током этой катушки. Магнитные цепи трансформаторов, электрических машин, измерительных приборов и других электрических аппаратов имеют более сложную форму.

Отдельные участки магнитных цепей могут изготавливаться из различных ферромагнитных материалов различной формы и раз­меров. Одним из участков магнитной цепи может быть воздуш­ный зазор.

Конструктивно различают неразветвленные и разветвленные магнитные цепи (рис. 8.1).

Характерной особенностью неразветвленной магнитной цепи (рис. 8.1., а) является то, что магнитный поток Ф, созданный токами обмоток для всех участков и сечений магнитной цепи, имеет одина­ковое значение (как ток в неразветвленной электрической цепи).

Для разветвленной магнитной цепи (рис. 8.1., б) характерно то, что созданный током магнитный поток Ф разветвляется, при этом его величина определяется алгебраической суммой магнит­ных потоков в разветвлениях 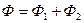(как и ток в разветвлен­ной электрической цепи - по первому закону Кирхгофа).

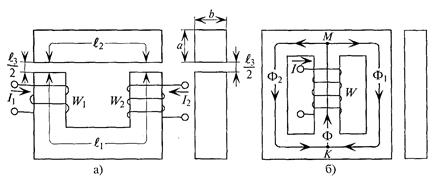
Рис. 8.1

Разветвленная магнитная цепь может быть симметричной или несимметричной. Цепь считается симметричной, если правая и левая ее части имеют одинаковые размеры, выполнены из одина­кового материала (включая воздушные зазоры) и действующие в каждой части магнитодвижущие силы IW одинаковы.

Магнитные цепи могут быть однородными и неоднородны­ми. Однородная магнитная цепь представляет собой замкнутый сердечник, который по всей длине l имеет одинаковое сечение S и выполнен из определенного материала.

Неоднородная магнитная цепь (рис. 8.1., а) состоит из нескольких однородных участков, каждый из которых по всей своей длине имеет одинаковое сечение и выполнен из определенного мате­риала.

На рис. 8.1., а изображена неразветвленная неоднородная магнит­ная цепь, состоящая из трех однородных участков длиной l₁, l₂ и l₃ где l₃ - воздушный зазор.

8.2. Закон Ома для магнитной цепи

Если по кольцевой катушке с числом витков W проходит ток I (рис. 7.8., а), то этот ток в сердечнике катушки длиной l и сечением S создает напряженность (7.19)

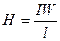
На рис. 7.8., а изображена однородная неразветвленная магнит­ная цепь, сердечник которой по всей длине l выполнен из одного материала с относительной магнитной проницаемостью μ_r. Тогда магнитный поток Ф в сердечнике кольцевой катушки можно определить по формуле

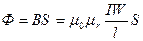(8.1)

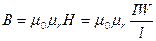где (8.2)

Это же уравнение (8.1) можно записать иначе:

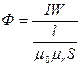
где числитель (IW) - магнитодвижущая сила, или магнитное напряжение магнитной цепи 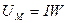, а знаменатель (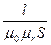) - магнитное сопротивление магнитной цепи (по аналогии с элек­трическим сопротивлением, зависящим от длины, удельной проводимости и сечения проводника), т. е.

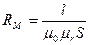(8.3)

Тогда магнитный поток магнитной цепи

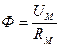(8.4)

Это и есть математическое выражение закона Ома для неразветвленной однородной магнитной цепи, т. е. магнитный поток в рассматриваемой магнитной цепи пропорционален магнитному напряжению 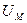и обратно пропор­ционален магнитному сопротивлению 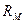(как и ток по закону Ома для участка электрической цепи).

Если неразветвленная цепь неоднородна и на сердечнике имеются две обмотки, т. е. две магнитодвижущие силы и три однородных участка (рис. 8.1., а), то закон Ома для такой маг­нитной цепи:

(8.5)

или иначе:

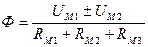(8.6)

(как и ток в неразветвленной электрической цепи с нескольки­ми источниками и несколькими сопротивлениями).

В выражениях (8.5) и (8.6) знак «плюс» между магнитными напряжениями ставят тогда, когда обмотки W₁ и W₂ (рис. 8.1., а) включены «согласно», т. е. создают магнитные потоки в сердеч­нике одного направления, а знак «минус» - когда обмотки вклю­чены «встречно», т. е. создают магнитные потоки в сердечнике, направленные друг против друга.

Из выражений (8.3) и (8.5) следует, что наибольшим сопро­тивлением в магнитной цепи обладает воздушный зазор R₃, так как относительная магнитная проницаемость его μ_r3 = 1, притом, что магнитная проницаемость ферромагнитных участков исчис­ляется десятками тысяч.

Как видно, законы в магнитной цепи для определения магнит­ного потока во многих случаях аналогичны законам в электри­ческих цепях для определения электрического тока, что в значи­тельной степени помогает при расчетах магнитных цепей.

Однако пользоваться законом Ома с использованием выраже­ний (8.4) и (8.5) для расчета магнитных цепей не представляется возможным, так как магнитная цепь нелинейная. Нелинейность магнитной цепи обусловлена тем, что магнитное сопротивление ферромагнитных участков магнитной цепи, определяющее маг­нитный поток, само зависит от магнитного потока.

Тем не менее, законы Ома для однородной и неоднородной цепи решают качественную задачу расчета цепей, т. е. зависимость па­раметров магнитных цепей друг от друга.

Расчет магнитных цепей производится с использованием зако­на полного тока.

8.3. Намагничивание ферромагнитных материалов

Так как ферромагнитный материал является основой магнитных цепей, то для исследования и расчета магнитных цепей необходимо изучить свойства и характеристики ферромагнитных материалов.

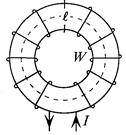
Рис. 8.2.

Если по катушке с числом витков W, распо­ложенной на замкнутом магнитопроводе дли­ной l, проходит ток I (рис. 8.2), то в катушке создается магнитное поле, напряженность ко­торого

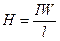
Если магнитопровод выполнен из нефер­ромагнитного материала, то индукция в маг­нитном поле магнитопровода .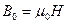

Если же магнитопровод катушки выполнен из ферромагнитного материала, то этот мате­риал намагничивается, т. е. происходит ориентация доменов ферро­магнитного материала в направлении внешнего магнитного поля, созданного магнитодвижущей силой катушки IW. Тем самым созда­ется добавочная магнитная индукция В_Д, обусловленная намагничива­нием ферромагнитного материала магнитопровода: 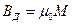, где М - величина, характеризующая намагниченность материала.

Таким образом, магнитная индукция В в магнитопроводе катушки складывается из двух компонентов - магнитной индукции внешне­го поля, созданной МДС катушки В₀, и добавочной индукции В_Д, созданной намагниченным магнитопроводом из ферромагнитного материала, т. е.

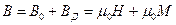(8.7)

Зависимость магнитных индукций В₀, В_Д и В от измене­ния напряженности Н пред­ставлена на рис. 8.3.

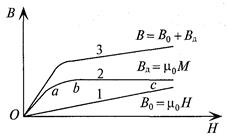
Рис. 8.3.

Зависимость В₀ = f(Н) - прямая линия из начала ко­ординат (прямая 1).

Характер изменения добавочной индукции В_Д = f(Н) можно объяснить следующим образом (кривая 2):

участок Оа - намагниченность сердечника М увеличивается пропорционально напряженности Н;

участок аb - рост намагниченности сердечника М замедляется, так как большинство доменов уже сориентировалось в направле­нии магнитного поля катушки;

участок bс - рост намагниченности сердечника М прекращает­ся, т. е. наступает режим магнитного насыщения, так как все до­мены сориентировались в направлении внешнего магнитного поля (участок bс параллелен оси абсцисс).

Суммарная кривая В = f(Н) строится путем сложения ординат кривых В₀ = f(Н) и В_Д = f(Н).

Суммарная кривая 3 зависимости индукции ферромагнитного материала от напряженности магнитного поля В = f(Н) называет­ся кривой намагничивания данного ферромагнитного материала.

Ферромагнитные материалы относятся к нелинейным средам, поэтому магнитные цепи, в которых они используются, являются нелинейными.

Магнитная проницаемость ферромагнитных материалов - ве­личина непостоянная и зависит от предварительного намагничи­вания, т. е. от напряженности поля, созданного в материале. Ха­рактер этой зависимости представлен кривой 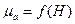(рис. 8.4).

Определить магнитную проницаемость ферромагнитного мате­риала при определенной напряженности Н или индукции В можно, воспользовавшись кривой намагничивания данного фер­ромагнитного материала:

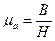(8-8)

8.4. Циклическое перемагничивание

Изменение тока в катушке (рис. 8.2) и соответственно напря­женности Н магнитного поля в ней не только по величине, но и по направлению приводит к изменению индукции в ферро­магнитном сердечнике катушки по величине и направлению (рис. 8.5).

Зависимость магнитной индукции В в сердечнике от напря­женности Н при изменении тока I катушки по величине и на­правлению можно проследить по кривой рис. 8.5.

Если в катушке находится полностью размагниченный сердеч­ник, то при токе I = 0, 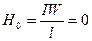(рис. 8.5).

Увеличение тока приводит к увеличению напряженности H, а следовательно, и индукции В в ферромагнитном материале до насыщения по кривой 0 - 1, т.е. по кривой намагничивания данного ферромагнитного материала (рис. 8.5). Если уменьшать ток до нуля, то и напряженность H уменьшается до нуля, а индук­ция при этом уменьшается от величины В_m (насыщение) до значения 0 - 2 по кривой 1 - 2. Значение индукции 0 - 2, оставшейся в сер­дечнике катушки (рис. 8.5) при уменьшении напряженности до H = 0, называется остаточной ин­дукцией B_r в данном ферромаг­нитном материале. Остаточная индукция в сердечнике B_r имеет место за счет того, что не все эле­ментарные магнитики материала дезориентировались при размаг­ничивании, т. е. часть доменов остались сориентированными в направлении внешнего поля ка­тушки.

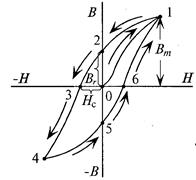
Рис. 8.5

Если изменить направление тока в катушке, а следовательно, и направление напряженности в сердечнике и увеличивать эту на­пряженность (в обратном направлении), то можно добиться уменьшения индукции до нуля (кривая 2 - 3), т. е. сердечник пол­ностью размагнитится. Напряженность 0 - 3, которая потребо­валась для того, чтобы размагнитить ферромагнитный материал, т. е. полностью дезориентировать домены, называется задержи­вающей, или коэрцитивной, силой Н_C.

Если продолжить увеличение напряженности, то индукция из­менит свое направление и ее значение будет увеличиваться в но­вом направлении от нуля до насыщения по кривой 3 - 4.

Если уменьшать напряженность до нулевого значения, то ин­дукция уменьшится по кривой 4 - 5, где отрезок 0 - 5 - остаточная индукция B_r в обратном направлении. Чтобы размагнитить сер­дечник, т. е. уменьшить индукцию до нуля, необходимо снова из­менить направление тока и напряженности (в первоначальном направлении) и увеличивать его. При этом индукция в сердечни­ке уменьшится до нуля по кривой 5 - 6, где отрезок 0 - 6 - задер­живающая, или коэрцитивная, сила Н_C в первоначальном направ­лении, которая снова размагничивает сердечник - уничтожает остаточную индукцию. Дальнейшее увеличение напряженности приведет к увеличению индукции от нуля до насыщения в перво­начальном направлении по кривой 6 - 1.

Кривая 0 - 1 называется кривой первоначального намагничива­ния, а замкнутая кривая 1 – 2 – 3 – 4 – 5 – 6 - 1 называется кривой циклического перемагничивания, или петлей гистерезиса. Гисте­резис - греческое слово, означающее «отставание», т. е. измене­ние индукции отстает от изменения напряженности: напряжен­ность уменьшилась до нуля, а индукция еще не равна нулю, или индукция только уменьшилась до нуля, а напряженность уже уве­личивается в обратном направлении.

Циклическое перемагничивание имеет место в магнитопроводах (сердечниках) электрических машин, трансформаторов, элек­троизмерительных приборов, дросселей и др., по обмоткам кото­рых проходит переменный ток.

Циклическое перемагничивание сопровождается затратой элек­трической энергии, которая преобразуется в тепловую и в боль­шинстве случаев рассеивается в пространстве. Такие тепловые потери относят к магнитным потерям Р_М и называют потерями энергии (мощности) на циклическое перемагничивание, или по­терями на гистерезис. Мощность потерь на циклическое перемаг­ничивание данного ферромагнитного материала пропорциональ­на площади, ограниченной петлей гистерезиса этого материала. Для борьбы с подобными потерями в различных аппаратах и ма­шинах применяют различные меры, основной из которых явля­ется выбор ферромагнитного материала для сердечников с узкой петлей гистерезиса.

Искусственно циклическое перемагничивание можно приме­нить для размагничивания ферромагнитного материала, т. е. для уменьшения остаточной индукции до нулевого значения. Для этого по катушке, расположенной на магнитопроводе из ферро­магнитного материала, пропускают изменяющийся по величине и направлению ток (переменный ток), величину которого посте­пенно уменьшают до нулевого значения.

8.5. Ферромагнитные материалы

Свойства большинства ферромагнитных материалов являются одинаковыми, однако проявляются они по-разному в зависимо­сти от химического состава материала. В этой связи различают две основные группы ферромагнитных материалов: а) магнит­но-мягкие и б) магнитно-твердые.

А. Магнитно-мягкие ферромагнитные материалы обладают вы­сокой магнитной проницаемостью (μ_r ≈ 10³ ÷ 10⁶), низкой задержива­ющей (коэрцитивной) силой (Н_C < 400 А/м) и узкой петлей гисте­резиса, т. е. малыми потерями на гистерезис.

Магнитно-мягкие ферромагнитные материалы легко намагни­чиваются и размагничиваются.

К магнитно-мягким материалам относятся металлы и сплавы: электролитическое железо, электротехническая сталь, пермаллой, ферриты, магнитодиэлектрики и др.

Железо и электротехническая сталь нашли широкое примене­ние для магнитных цепей электрических машин, аппаратов, трансформаторов, электроизмерительных приборов, т. е. там, где необходимо создать сильное магнитное поле при относительно небольших магнитодвижущих силах (IW).

Ферриты и магнитодиэлектрики применяются в качестве магнитопроводов в аппаратуре проводной и радиосвязи, в магнитных усилителях, вычислительных машинах и других видах техники.

Пермаллой используется при изготовлении сердечников, пред­назначенных для работы в высокочастотных устройствах до 50 000 кГц. Магнитные свойства пермаллоев в значительной сте­пени зависят от технологии их изготовления.

Б. Магнитно-твердые ферромагнитные материалы обладают незначительной магнитной проницаемостью (μ_r - порядка не­скольких сотен), относительно высокой остаточной индукцией В_r ≈ (0,3 ÷ 125) Тл, большой задерживающей (коэрцитивной) силой Н_C ≈ (5000 ÷ 240 000) А/м и имеют широкую петлю гистерезиса.

Из магнитно-твердых материалов изготавливаются постоянные магниты, применяемые в технике связи, электроизмерительной технике и т. п.

К магнитно-твердым материалам, обладающим лучшими маг­нитными свойствами, относятся такие сплавы, как альни, альниси, альнико и др.

Дата добавления: 2015-08-02