
Читайте также:
|
Пусть символ  обозначает число, квадрат которого равен
обозначает число, квадрат которого равен  , т.е.
, т.е.
 .
.
Символ  называют мнимой единицей. Выражение вида
называют мнимой единицей. Выражение вида  , где
, где  – действительные числа, называют комплексным числом. При этом,
– действительные числа, называют комплексным числом. При этом,  называют действительной частью числа
называют действительной частью числа  ,
,  – его мнимой частью. Действительную и мнимую части числа
– его мнимой частью. Действительную и мнимую части числа  обозначают обычно
обозначают обычно  и
и  соответственно, т.е.
соответственно, т.е. 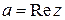 и
и 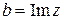 .
.
Комплексное число вида 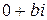 (где
(где 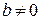 ) принято называть чисто мнимым и записывать в виде
) принято называть чисто мнимым и записывать в виде  . Комплексные числа
. Комплексные числа  и
и  (т.е. числа, которые отличаются только знаком мнимой части), называют комплексно сопряженными. Если одно из этих чисел обозначено через
(т.е. числа, которые отличаются только знаком мнимой части), называют комплексно сопряженными. Если одно из этих чисел обозначено через  , то другое принято обозначать
, то другое принято обозначать  .
.
Пусть  ,
,  . Комплексные числа
. Комплексные числа  и
и 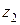 называются равными (записывают:
называются равными (записывают:  ), если соответственно равны их действительные и мнимые части, т.е. если
), если соответственно равны их действительные и мнимые части, т.е. если  и
и  . При этом полагают, что
. При этом полагают, что  и
и  .
.
Последнее равенство позволяет рассматривать действительные числа как подмножество множества комплексных чисел.
Всякое комплексное число  можно изобразить на плоскости
можно изобразить на плоскости 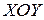 в виде точки
в виде точки  . Причем соответствие между комплексными числами и точками плоскости
. Причем соответствие между комплексными числами и точками плоскости 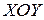 будет взаимно однозначным. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью. Ось
будет взаимно однозначным. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью. Ось  комплексной плоскости называют действительной осью, так как точкам оси
комплексной плоскости называют действительной осью, так как точкам оси  соответствуют действительные числа. Точки, лежащие на оси
соответствуют действительные числа. Точки, лежащие на оси  , изображают чисто мнимые числа. Поэтому ось
, изображают чисто мнимые числа. Поэтому ось  комплексной плоскости называют мнимой осью.
комплексной плоскости называют мнимой осью.
Расстояние от точки  комплексной плоскости до начала координат
комплексной плоскости до начала координат  , называют модулем комплексного числа
, называют модулем комплексного числа  и обозначают
и обозначают  . Очевидно, что
. Очевидно, что 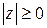 и
и  .
.
Величину  угла между вектором
угла между вектором  и действительной осью
и действительной осью  называют аргументом комплексного числа (при этом
называют аргументом комплексного числа (при этом  берут со знаком «плюс» если поворот от оси
берут со знаком «плюс» если поворот от оси  к вектору
к вектору  осуществляется против часовой стрелки, и со знаком «минус» – в противном случае). Очевидно, что аргумент данного комплексного числа
осуществляется против часовой стрелки, и со знаком «минус» – в противном случае). Очевидно, что аргумент данного комплексного числа  (
( ) определен неоднозначно, причем любые два значения аргумента отличаются на величину, кратную
) определен неоднозначно, причем любые два значения аргумента отличаются на величину, кратную  . Множество значений аргумента числа
. Множество значений аргумента числа  обозначают
обозначают  ; значение аргумента, принадлежащее промежутку
; значение аргумента, принадлежащее промежутку  , обозначают
, обозначают  и называют главным значением аргумента. Для
и называют главным значением аргумента. Для  аргумент не определен.
аргумент не определен.
 Пусть Пусть 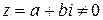 , ,  , ,  – аргумент – аргумент  . Очевидно, что . Очевидно, что
 , ,  .
Но тогда комплексное число .
Но тогда комплексное число  можно записать в виде можно записать в виде
| 
 

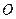 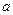 
|
 .
.
Запись комплексного числа в виде  принято называть алгебраической формой записи комплексного числа, а запись в виде
принято называть алгебраической формой записи комплексного числа, а запись в виде  – тригонометрической формой записи.
– тригонометрической формой записи.
На практике нередко приходится переходить от одной формы записи комплексного числа к другой. Такой переход не представляет трудности. Действительно, если число  записано в виде
записано в виде  , то его действительная часть
, то его действительная часть  и мнимая часть
и мнимая часть  находятся по формулам:
находятся по формулам:

 ,
,  .
.
Если число  записано в виде
записано в виде  , то его модуль
, то его модуль  и аргумент
и аргумент  находятся по формулам
находятся по формулам
 ,
, 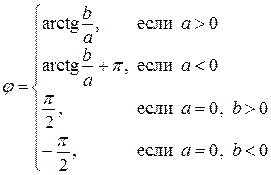
Пример.
1) Записать 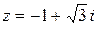 в тригонометрической форме.
в тригонометрической форме.
Находим модуль  и аргумент
и аргумент  комплексного числа. Так как его действительная часть
комплексного числа. Так как его действительная часть  и мнимая часть
и мнимая часть  , то
, то
 и
и  .
.
Следовательно, 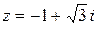
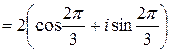 .
.
2) Записать число  в алгебраической форме.
в алгебраической форме.
Находим действительную и мнимую части числа  . Так как его модуль
. Так как его модуль  , а аргумент
, а аргумент 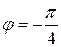 , то
, то

 ,
, 
 .
.
Следовательно,  .
.
Дата добавления: 2015-08-02; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Кучкин В.А., Даниил Московский | | | Действия над комплексными числами в алгебраической форме |