В любой точке потенциальная энергия заряда численно равна работе, которую необходимо затратить для перемещения заряда в эту точку.

Подобно тому, как потенциальная энергия в поле сил тяготения пропорциональна массе тела, потенциальная энергия электростатического поля пропорциональна заряду:

Е_п = φq (10)

Величина φ = E_п/q (11)

называется электрическим потенциалом поля.

Она характеризует потенциальную энергию, которой обладал бы положительный единичный заряд, помещённый в данную точку поля.

Для того, чтобы вычислить полную потенциальную энергию заряда, надо найти работу сил поля по перемещению заряда из данной точки поля в точку, где поле отсутствует, например на бесконечно большое расстояние от зарядов, создающих поле:

А = -ΔЕ_п = -(Е_п2 - Е_п1) = q(φ₁ – φ₂) (12)

Величину (φ₁ – φ₂) называют разностью потенциалов электростатического поля. Понятие разности потенциалов (или напряжения) применимо лишь к двум различным точкам поля.

[φ] = 1В = 1Дж/Кл

Потенциал является энергетической характеристикой электростатического поля и может принимать положительные и отрицательные значения. Физический смысл имеет разность потенциалов, т.к. через неё выражается работа сил поля по перемещению заряда.

Значение потенциала может быть определено лишь по отношению к определённому уровню, принятому за нулевой, в то время как на значение разности потенциалов он не влияет.

Потенциал электростатического поля точечного заряда Q в точке, удалённой на расстояние r от заряда:

φ = kQ/r (13)

Эта формула справедлива при условии, что потенциал стремится к нулю при r →∞.

Формулой (13) можно пользоваться для определения потенциала поля шара радиусом R и зарядом Q, равномерно распределённым по его поверхности (r>R).

Внутри шара имеется постоянный потенциал поля, равный

φ = kQ/R (14)

Графически электрическое поле можно изображать не только с помощью линий напряжённости, но и с помощью эквипотенциальных поверхностей – совокупностей точек, имеющих одинаковый потенциал. Пересекаясь с плоскостью чертежа, эквипотенциальные поверхности дают эквипотенциальные линии.

На нижних рисунках изображены эквипотенциальные поверхности точечного и плоского зарядов.

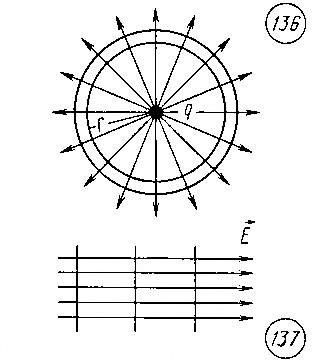
Свойства эквипотенциальных поверхностей:

1) В каждой точке эквипотенциальной поверхности вектор напряжённости поля перпендикулярен ей и направлен в сторону убывания потенциала.

2) Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

Исходя из свойств эквипотенциальных поверхностей можно по известному расположению эквипотенциальных поверхностей в каждой точке поля определить направление вектора напряжённости или по известному расположению линий напряжённости можно построить эквипотенциальные поверхности.

3 Связь между напряжённостью и разностью потенциалов.

Каждой точке электрического поля соответствуют определенные значения потенциала и напряженности. Найдем связь напряженности электрического поля с потенциалом.
Пусть заряд q перемещается в направлении вектора напряженности однородного электрического поля 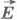из точки 1 в точку 2, находящуюся на расстоянии от точки 1 (рис.14.28). Электрическое поле совершает работу:

A = qEΔd

Эту работу согласно формуле (12) можно выразить через разность потенциалов в точках 1 и 2:

А = q(φ₁ – φ₂) = qU

Приравнивая выражения для работы, найдем модуль вектора напряженности поля:

E = U/Δd (15)

В этой формуле U - разность потенциалов между точками 1 и 2, которые связаны вектором перемещения , совпадающим по направлению с вектором напряженности 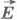(см. рис.14.28).
Формула (15) показывает: чем меньше меняется потенциал на расстоянии , тем меньше напряженность электростатического поля. Если потенциал не меняется совсем, то напряженность поля равна нулю.
Так как при перемещении положительного заряда в направлении вектора напряженности электростатическое поле совершает положительную работу , то потенциал больше потенциала .
Следовательно, напряженность электрического поля направлена в сторону убывания потенциала.
Любое электростатическое поле в достаточно малой области пространства можно считать однородным. Поэтому формула (15) справедлива для произвольного электростатического поля, если только расстояние настолько мало, что изменением напряженности поля на этом расстоянии можно пренебречь.
Единица напряженности электрического поля. Единицу напряженности электрического поля в СИ устанавливают, используя формулу (15). Напряженность электрического поля численно равна единице, если разность потенциалов между двумя точками на расстоянии 1 м в однородном поле равна 1 В. Наименование этой единицы - вольт на метр (В/м).
Напряженность можно также выражать в ньютонах на кулон. Действительно,

Дата добавления: 2015-08-02