Сгущение геодезической сети дополнительными пунктами

СГУЩЕНИЕ ГЕОДЕЗИЧЕСКОЙ СЕТИ ДОПОЛНИТЕЛЬНЫМИ ПУНКТАМИ

Методические указания к выполнению лабораторной

Работы

Москва 2005 г.

Методичесие указания одобрены и рекомендованы к изданию

кафедрой геодезии и геоинформатики

Государственного университета по землеустройсту

(Протокол №1 от 7.02.2002 г.)

СГУЩЕНИЕ ГЕОДЕЗИЧЕСКОЙ СЕТИ ДОПОЛНИТЕЛЬНЫМИ ПУНКТАМИ

Дополнительные (одиночные) пункты определяют для сгущения геодезической сети методами прямой и обратной за­сечек, а при наличии электромагнитных дальномеров - методом линейной засечки, а также лучевым методом. В некоторых слу­чаях для привязки полигонометрических (теодолитных) ходов дополнительные пункты определяют методом снесения коор­динат с вершины знака на землю.

Для выполнения данной работы студент по заданию препода­вателя должен решить задачи:

1.Снесение координат с вершины знака на землю.

2.Вычисление координат прямой засечки по формулам Юнга.

3.Вычисление координат прямой засечки по формулам Гаусса.

4.Вычисление координат обратной засечки.

5.Вычисление координат линейной засечки.

6.Вычисление координат пунктов, определяемых лучевым методом.

1. Снесение (передача) координат с вершины знака на землю.

Эта задача возникает в том случае, когда требуется произвес­ти привязку полигонометрического (теодолитного) хода к пункту А с известными координатами вершины знака (рис.1), на который нельзя стать с прибором (например, пункт А - шпиль башни). Для выполнения привязки хода выбирают вблизи пункта А на земле пункт Р в таком месте, чтобы с него был виден пункт А и два удаленных исходных пункта В и С (один из них для контроля определения коор­динат пункта Р).

Сущность задачи заключается в передаче координат с пункта А на пункт Р.

Для решения задачи (с контролем) измеряют два базиса в, в' и шесть углов: β₁, β₂, 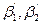, δ, δ’ (рис. 1), причём второй базис и углы при нём используют для контроля определения расстояния АР = d и повышения точности его окончательного значения, а угол δ’- для контроля правильности произведённых измерений и повышения точности определения координат пункта Р.

рис.1

Второе решение задачи, с участием базиса в' и координат пункта С (вместо В) производят по аналогичным формулам.

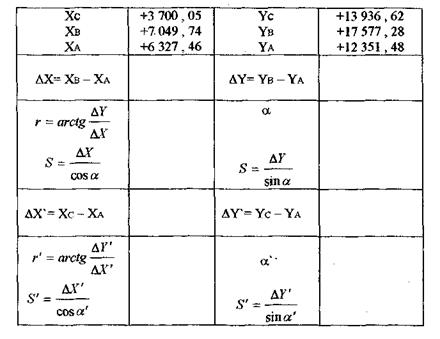
Вычисления выполняют по приведенным схемам.

1.Вычисление α, α', S, S'.

Значения α и α' вычисляют до секунд.

При вычислении S и S^’ могут получаться большие расхождения (до 0,10 м). Убедившись в правильности вычислений, за окончатель­ное значение S или S' следует взять полученное по большему (по абсолют­ной величине) значению разности координат. Окончательный результат подчеркивают.

2. Прямая засечка

Сущность задачи состоит в определении координат третьего пункта по координатам двух исходных и двум измеренным углам при этих пунктах. Для контроля определения измеряют еще угол при третьем исходном пункте.

В зависимости от того, какие углы измерены, задачу решают либо по формулам Юнга, либо по формулам Гаусса.

Дата добавления: 2015-08-10