Генетическое равновесие популяции

Как свидетельствуют вышеупомянутые расчеты, соотношение генотипов в каждой популяции должно быть на характерном для нее уровне. Таким образом, каждая популяция находится в определенном равновесии по аллельным генам в изучаемом локусе.

Генетическое равновесие популяции выражается формулой ГАРДИ ВАЙНБЕРГА: р²АА + 2рqАа + q²аа = 1

Метод позволяет установить, отвечает ли фактическое распределение фенотипов и генотипов определенной популяции теоретически ожидаемому. Как можно изменить соотношение генотипов и фенотипов в популяции, если вести определенный отбор.

Пример: У лошадей чистокровной верховой породы носовое кровотечение предопределено рецессивным геном _„а”. В конном заводе среди 5400 голов 17 лошадей болели носовым кровотечением и погибли после соревнований. Нужно установить, сколько животных в популяции являются носителями этого гена, и какая вероятность появления лошадей с носовым кровотечением в последующих поколениях при свободном спаривании фенотипически здоровых животных?

Частота генотипа

Частота алеля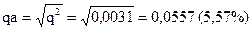

Частота алеля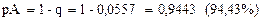

Частота генотипа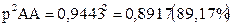

Частота генотипа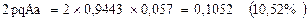

Таким образом, в 89,17% животных (генотип АА) отсутствует ген носового кровотечения (4815 голов), 10,52% животных (генотип Аа) являются носителями этого гена (568 голов) и 0,31 % животных (генотип аа) будут больными (17 голов).

Если проводить элиминацию животных с генотипом „аа”, то структура популяции изменится.

Частоты генов „А” и „а” будут составлять:

Отсюда появление животных с носовым кровотечением (генотип аа) будет составлять 0,0028 или 0,28%, что на 0,03% ниже, чем в предыдущем поколении. Количество животных носителей летального гена также снизится до 10,00% против 10,52 %.

Дата добавления: 2015-08-10