
|
Читайте также: |
Расчет коэффициента фенотипической корреляции.
Задание 1.
Необходимо выяснить: целесообразно ли вести отбор коров только за величиной надоя за лактацию, не учитывая жирномолочность; существует ли между этими признаками взаимосвязь?
Для решения этого вопроса методом случайного отбора из группы коров хозяйства отбирают группу для проведения биометрического анализа. Параметры продуктивности этой выборки приведены в таблице 1.
Параметры продуктивности животных. Таблица 1.
| Кличка коров | Лактация | Надежд коров за 305 дней лактации, кг | Среднее содержание жира в молоке % |
| Ария | ІІІ | 4,1 | |
| Березка | ІІІ | 3,7 | |
| Соя | ІІІ | 4,0 | |
| Синька | IV | 3,8 | |
| Слива | ІІІ | 3,6 | |
| Полька | IV | 3,6 | |
| Майка | Ш | 3,9 | |
| Алиса | IV | 3,7 | |
| Абрикос | Ш | 3,7 | |
| Белка | V | 3,7 |
Алгоритм расчета.
1. Для облегчения расчетов многозначные числовые варианты сокращаем в 1000 раз (100, 10), а результаты округляем (3840:1000=3,8).
2. Строим расчетную таблицу и записываем в неё варианты первого и второго признаков („x” – удой, „y” - жирномолочность). Параметры приведены в таблице 2.
Корреляционная решетка. Таблица 2.
| № | „x” удой | „y” жирно молочность | Преобразованные значения признаков | Значения преобразованных признаков возведены в квадрат | Разница между значениями | Квадрат разницы | ||
| x | у | |||||||
| Vх | Vу | Vх | Vу | 
| 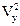
| d=Vх - Vу | d2 | |
| 4,1 | 3,8 | 4,1 | 16,44 | 16,81 | -03 | 0,09 | ||
| 3,7 | 3,7 | 18,48 | 13,69 | 0,6 | ||||
| 4,0 | 3,4 | 4,0 | 16,00 | -0,6 | ||||
| 3,8 | 4,1 | 3,8 | 16,81 | 14,44 | 0,09 | |||
| 3,6 | 4,6 | 3,6 | 21,16 | 12,96 | 1,0 | 1,00 | ||
| 3,6 | 5,1 | 3,6 | 26,01 | 12,96 | 1,5 | 2,25 | ||
| 3,9 | 3,9 | 3,9 | 15,21 | 15,21 | ||||
| 3,7 | 4,9 | 3,7 | 24,01 | 13,69 | 1,2 | 1,44 | ||
| 3,7 | 4,5 | 3,7 | 20,25 | 13,69 | 0,8 | 0,64 | ||
| 3,7 | 4,7 | 3,7 | 22,09 | 13,69 | 1,0 | 1,00 | ||
| ∑ | 43,3 | 37,8 | 190,02 | 142,14 | 5,5 | 7,23 |
3. Проводим расчет дисперсий:

4. Проводим расчет коэффициента корреляции:

5. Определяем статистическую ошибку:
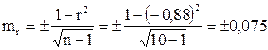
6. Определяем критерий достоверности:

при числе ν = n - 2 = 10 - 2 = 8, по таблице Стьюдента находим вероятность полученных результатов Р > 0,999.
Вывод: Между величиной удоя и содержанием жира в молоке коров установленная сильная обратная корреляция. Это значит, что если вести отбор только по признаку удоя, то среднее содержание жира в молоке в группе следующих поколений будет снижаться.
ІІ. Расчет коэффициента корреляции для альтернативных признаков.
Дата добавления: 2015-08-10; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ТЕОРЕТИЧЕСКОЕ OБОСНОВАНИЕ. | | | ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ |