Определение устойчивости по корням характеристического уравнения.

Критерий устойчивости Гурвица

clc

T2=0.03;

T3=0.1;

W1=tf([5],[0.005 1]);

W2=tf([1],[T2^2 2*0.8*T2 1]);

W3=tf([1],[T3 1]);

Wraz=W1*W2*W3;

Wzam=feedback(Wraz,1);

Transfer function:

--------------------------------------------------------

4.5e-007 s^4 + 0.0001185 s^3 + 0.00644 s^2 + 0.153 s + 1

Transfer function:

--------------------------------------------------------

4.5e-007 s^4 + 0.0001185 s^3 + 0.00644 s^2 + 0.153 s + 6

A1=[0.0001185]

A2=[0.0001185 0.153; 0.00000045 0.00644 ]

A3=[0.0001185 0.153 0; 0.00000045 0.00644 6; 0 0.0001185 0.153]

A4=[0.0001185 0.153 0 0; 0.00000045 0.00644 6 0;0 0.0001185 0.153 0; 0 0.00000045 0.00644 6]

delta1=det(A1)

delta2=det(A2)

delta3=det(A3)

delta4=det(A4)

A1 =

1.1850e-004

A2 =

0.0001 0.1530

0.0000 0.0064

A3 =

0.0001 0.1530 0

0.0000 0.0064 6.0000

0 0.0001 0.1530

A4 =

0.0001 0.1530 0 0

0.0000 0.0064 6.0000 0

0 0.0001 0.1530 0

0 0.0000 0.0064 6.0000

delta1 = 1.1850e-004

delta2 = 6.9429e-007

delta3 = 2.1973e-008

delta4 = 1.3184e-007

Все определители Гурвица одного знака с первым коэффициентом (а ₀) характеристического уравнения (больше нуля), следовательно система устойчива.

Критерий устойчивости Михайлова.

w=-5:1:40;

s=j*w;

D=0.00000045*s.^4+0.0001185*s.^3+0.00644*s.^2+0.153*s+6;

Re=real(D);

Im=imag(D);

figure(1)

plot(Re,Im),grid

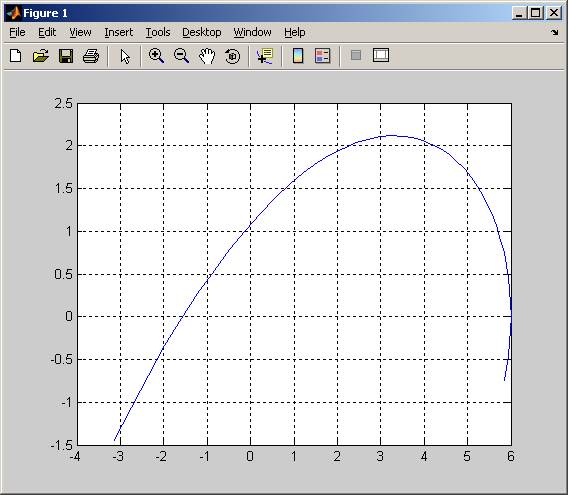
Определение устойчивости по корням характеристического уравнения.

figure(2)

pzmap(Wzam),grid

Дата добавления: 2015-08-10