
Читайте также:
|
Решение задачи прицеливания при стрельбе из
Для определения параметров прицеливания при стрельбе из неподвижного оружия изобразим векторную схему прицеливания для этого случая (рис.1).

Pиc.1
В точке О находится самолет-истребитель, атакующий цель, находящуюся в точке Ц и движущуюся со скоростью 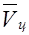 . Вектор
. Вектор  – фактическая дальность до цели. Истребитель имеет скорость
– фактическая дальность до цели. Истребитель имеет скорость  . Оружие на нем установлено по продольной оси. Между скоростью
. Оружие на нем установлено по продольной оси. Между скоростью  и начальной скоростью снаряда относительно самолета
и начальной скоростью снаряда относительно самолета  имеется угол
имеется угол  из-за наличия углов атаки
из-за наличия углов атаки  и скольжения
и скольжения 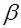 . Следует сказать, что при решении задачи прицеливания все используемые углы рассматриваются как векторные величины. Модулем такого вектора является величина угла, а за линию его направления принимается перпендикуляр к плоскости, в которой расположен угол. Поэтому можно записать, что
. Следует сказать, что при решении задачи прицеливания все используемые углы рассматриваются как векторные величины. Модулем такого вектора является величина угла, а за линию его направления принимается перпендикуляр к плоскости, в которой расположен угол. Поэтому можно записать, что 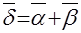 . Абсолютная начальная скорость, снаряда
. Абсолютная начальная скорость, снаряда  Модуль этой скорости
Модуль этой скорости
 . (1)
. (1)
Вектор выноса визирного устройства относительно оружия равен нулю, следовательно, визирное устройство (ВУ) и оружие находятся в точке О. Точкой прицеливания является цель, в которую должен попасть снаряд. Следовательно, вектор выноса точки прицеливания и вектор выноса точки разрыва снаряда также равны нулю. Истребитель имеет такое направление полета, при котором цель не может быть поражена, т.е. прицеливание не выполнено. Цель, находящаяся на дальности Dц и имеющая скорость  , может быть поражена, если будет находиться в точке
, может быть поражена, если будет находиться в точке  , вектор дальности до которой равен
, вектор дальности до которой равен  , при этом D=Dц. Кроме того на векторной схеме обозначено:
, при этом D=Dц. Кроме того на векторной схеме обозначено:  - точка, где будет цель в момент попадания в нее снаряда;
- точка, где будет цель в момент попадания в нее снаряда; 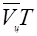 - вектор перемещения цели за время полета снаряда Т от момента выстрела до момента попадания в цель (при условии, что в момент выстрела цель будет находиться в точке Цу;
- вектор перемещения цели за время полета снаряда Т от момента выстрела до момента попадания в цель (при условии, что в момент выстрела цель будет находиться в точке Цу;  - вектор перемещения снаряда за время Т в направлении вектора
- вектор перемещения снаряда за время Т в направлении вектора  ;
;  - дальность полета снаряда в направлении вектора
- дальность полета снаряда в направлении вектора  за время Т;
за время Т; 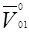 - орт вектора
- орт вектора  ,
,
 ; (2)
; (2)
 - вектор понижения снаряда за время Т из-за действия на снаряд силы тяжести;
- вектор понижения снаряда за время Т из-за действия на снаряд силы тяжести;  - упрежденная дальность до цели (вектор перемещения снаряда за время Т);
- упрежденная дальность до цели (вектор перемещения снаряда за время Т);  и
и  – углы, определяющие положения векторов
– углы, определяющие положения векторов  и
и  относительно оси самолета.
относительно оси самолета.
Так как цель в данном случае не может быть поражена, то имеется ошибка прицеливания (промах), которую можно выразить углом  , (принято во внимание, что D=Dц).Каждый из углов в формуле для определения промаха представим в виде двух составляющих, являющихся углами поворота для перехода из связанной системы координат
, (принято во внимание, что D=Dц).Каждый из углов в формуле для определения промаха представим в виде двух составляющих, являющихся углами поворота для перехода из связанной системы координат 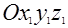 (системы “1”) в систему координат
(системы “1”) в систему координат  (систему “ D ”), связанную с вектором дальности. На рис.2 показана последовательность поворотов на углы jy и jz системы “1” для перехода в систему “ D ”. Тогда формула для определения промаха будет иметь следующий вид:
(систему “ D ”), связанную с вектором дальности. На рис.2 показана последовательность поворотов на углы jy и jz системы “1” для перехода в систему “ D ”. Тогда формула для определения промаха будет иметь следующий вид:

Рис.2
 .
.
Отсюда следует, что промах может быть определён в скалярном виде по формулам: Δ jy = jцy - jy, Δ jz = jцz - jz.
Ошибки Δ jy и Δ jz называются параметрами прицеливания. Величины Dц, jцy, jцz являются фактическими координатами цели, а величины D, jy, jz – это требуемые координаты цели (координаты точки Цтр). Фактические координаты цели могут быть определены с помощью систем сопровождения цели (ССЦ), а углы jy, jz должны быть вычислены. Для вычисления этих углов на основании схемы прицеливания (рис 1) составим векторное уравнение:
 +
+ 

 , (3)
, (3)
Для определения скорости цели  примем гипотезу
примем гипотезу  =const и применим формулу
=const и применим формулу
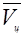 =
=  +
+ 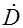
 +
+  . (4)
. (4)
В формуле (4) стоит вектор `D, а не вектор `Dц,так как скорость цели определяется при условии, что цель находится в точке Цу. Перепишем уравнение (3) с учетом (2) и (4)

 +
+  +
+ 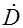
 +
+ 

 . (5)
. (5)
Каждый вектор в этом уравнении зададим в такой системе координат, в которой легко находятся его проекции. Вектор  зададим в системе координат
зададим в системе координат  , вектор
, вектор  – в скоростной системе координат
– в скоростной системе координат  , вектор
, вектор  – в связанной системе координат
– в связанной системе координат 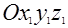 , вектор
, вектор  – в нормальной системе координат
– в нормальной системе координат  . Тогда
. Тогда 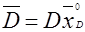 ,
,  ,
,  ,
,  ,
,  и уравнение (6) будет иметь вид:
и уравнение (6) будет иметь вид:
 +
+ 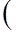
 +
+ 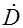
 +
+ 

 , (6)
, (6)
В уравнении (6) имеются две неизвестные величины:  и
и  . Величины Т и
. Величины Т и  являются баллистическими функциями от аргументов
являются баллистическими функциями от аргументов  , с,
, с, 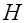 и
и  , где с – баллистический коэффициент снаряда, а
, где с – баллистический коэффициент снаряда, а 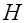 – высота полета. Вектор
– высота полета. Вектор  определяется углами атаки a и скольжения b, а вектор
определяется углами атаки a и скольжения b, а вектор  - углами крена g и тангажа u. Скорость V 01может быть определена по формуле (1). Скорость
- углами крена g и тангажа u. Скорость V 01может быть определена по формуле (1). Скорость 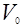 и баллистический коэффициент c являются техническими характеристиками оружия, а параметры
и баллистический коэффициент c являются техническими характеристиками оружия, а параметры  измеряются в полете соответствующими устройствами. Направление орт–вектора
измеряются в полете соответствующими устройствами. Направление орт–вектора  задаётся углами
задаётся углами  и
и  , которые могут быть определены, если при решении уравнения (6) будет применена матрица
, которые могут быть определены, если при решении уравнения (6) будет применена матрица  . Таким образом, в уравнении (6) неизвестными являются три скалярных величины
. Таким образом, в уравнении (6) неизвестными являются три скалярных величины  ,
,  и
и  . Для их определения необходимы три скалярных уравнения, которые можно получить, проектируя уравнение (6) на оси системы
. Для их определения необходимы три скалярных уравнения, которые можно получить, проектируя уравнение (6) на оси системы  , являющейся самой удобной для этой цели. При проектировании будем учитывать, что
, являющейся самой удобной для этой цели. При проектировании будем учитывать, что 
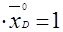 ,
,  ,
,
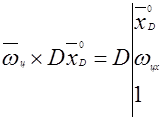


 .
.
В результате проектирования получим следующую систему уравнений:
 ,
,
 , (7)
, (7)
 .
.
В этой системе уравнений скалярные произведения орт–векторов будем определять, используя выражение из векторной алгебры:
 . (8)
. (8)
Для этого необходимо векторы, входящие в скалярное произведение, задать в одной системе координат. Зададим все орт-векторы в уравнениях (7) в системе координат “1”, переход к которой производится по формуле
 , (9)
, (9)
Используя эту формулу, можно получить следующие выражения:

 (10)
(10)
где  ;
;  -
- 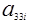 – элементы матрицы
– элементы матрицы  . Матрицы
. Матрицы 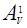 ,
, 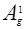 и
и  имеют вид:
имеют вид:


 , (11)
, (11)


 , (12)
, (12)



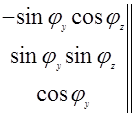 . (13)
. (13)
Так как скалярные произведения векторов в уравнениях (7) – это проекции ортов  ,
,  ,
,  на оси координат системы “ D ”, то любое из этих произведений можно представить в виде
на оси координат системы “ D ”, то любое из этих произведений можно представить в виде  , где m,n=x,y,z, а i=V,g, 1. Тогда на основании формул (10) можно записать:
, где m,n=x,y,z, а i=V,g, 1. Тогда на основании формул (10) можно записать:
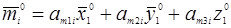 ,
,  , (14)
, (14)
где аm1i, аm2i, аm3i, - элементы матрицы той строки, в которой стоит значение орта 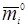 ; аn1D, аn2D, аn3D, - элементы матрицы той строки, в которой стоит значение орта
; аn1D, аn2D, аn3D, - элементы матрицы той строки, в которой стоит значение орта  .
.
Тогда на основании формул (8) и (14) выражение для  будет иметь следующий вид:
будет иметь следующий вид:
 (15)
(15)
Применим равенство (15) для определения, например, скалярного произведения  . Пользуясь матрицами
. Пользуясь матрицами 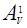 и
и  находим, что
находим, что
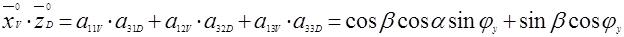 .
.
Аналогично определяются и другие скалярные произведения векторов в уравнениях системы (7).
На основании вышеизложенного можно получить следующую систему уравнений для решения задачи прицеливания из неподвижного оружия:
1) 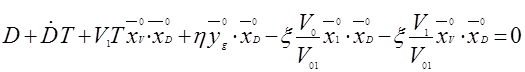 ,
,
2)  ,
,
3)  ,
,
4) 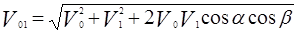 ,
,
5) 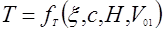 ,
,
6)  ,
,
7) 
8)  ,
,
9)  ,
,
10) 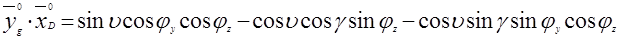 ,
,
11)  ,
,
12)  ,
,
13)  ,
,
14)  ,
,
15)  .
.
Разрешая последнюю систему уравнений относительно неизвестных величин, можно определить углы  и
и  , которые могут использоваться для обозначения на индикаторе лётчика требуемого положения цели. Для сведения ошибки прицеливания
, которые могут использоваться для обозначения на индикаторе лётчика требуемого положения цели. Для сведения ошибки прицеливания  к нулю необходимо разворотом самолета совместить точку Цтр с целью.
к нулю необходимо разворотом самолета совместить точку Цтр с целью.
Следует сказать, что из системы уравнений для решения задачи прицеливания ни одна из неизвестных величин не может быть определена в явном виде. Поэтому такая система решается методом итераций. Для решения этой системы требуется выполнить большое количество арифметических действий и определить значения тригонометрических функций многих углов. Для сокращения указанных операций при решении уравнений системы в них производят упрощения, незначительно влияющие на точность вычисления. Так синусы малых углов заменяют значениями самих углов, а косинусы таких углов приравнивают к единице. Слагаемое или несколько слагаемых, которые очень мало влияют на результат, как правило, исключают. Такими слагаемыми могут быть произведения, в которых имеется два и более сомножителя, являющиеся синусами малых углов. Если слагаемое или группа слагаемых при изменении параметров изменяют свои значения в небольших пределах, то это слагаемое или группу слагаемых заменяют постоянной величиной, равной среднему их значению
Произведем упрощения в итоговой системе уравнений. Будем считать, что углы  ,
,  ,
,  и
и  , малы, так как из этих углов наибольшее максимальное значение имеет угол
, малы, так как из этих углов наибольшее максимальное значение имеет угол 
 , а
, а  ,
,  . Поэтому считаем, что косинусы этих углов равны единице, их синусы равны значениям самих углов, а произведения двух и более синусов этих углов равны нулю. Кроме того значения понижения снаряда η составляют несколько метров, что значительно меньше дальности до цели D, составляющей сотни метров. Поэтому в первом уравнении системы слагаемое
. Поэтому считаем, что косинусы этих углов равны единице, их синусы равны значениям самих углов, а произведения двух и более синусов этих углов равны нулю. Кроме того значения понижения снаряда η составляют несколько метров, что значительно меньше дальности до цели D, составляющей сотни метров. Поэтому в первом уравнении системы слагаемое  можно не учитывать. Следует сказать, что максимальное значение величины
можно не учитывать. Следует сказать, что максимальное значение величины  может быть тогда, когда самолет атакует цель по линии близкой к вертикали, а это маловероятно. Обычно, наиболее вероятные значения углов между векторами
может быть тогда, когда самолет атакует цель по линии близкой к вертикали, а это маловероятно. Обычно, наиболее вероятные значения углов между векторами 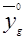 и
и  лежат в диапазоне, где
лежат в диапазоне, где  . После упрощений выражения для скалярных произведений векторов будут такие:
. После упрощений выражения для скалярных произведений векторов будут такие:
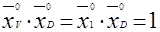 ,
,  ,
, 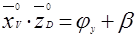 ,
,
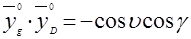 ,
,  ,
,

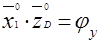 .
.
Учитывая эти выражения и принимая  ,
, 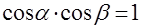 , система уравнений для решения задачи прицеливания может быть приведена к следующему виду:
, система уравнений для решения задачи прицеливания может быть приведена к следующему виду:
 ,
,
 ,
,
 ,
,
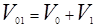 ,
,
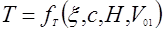 ,
,
 .
.
Такая система уравнений для решения задачи прицеливания с несущественными изменениями применяется в прицеле АСП – 17МЛ.
Дата добавления: 2015-08-10; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Последующие действия | | | Аннотация |