Полиспастах крана

В качестве редуцирующих узлов грузоподъемных механизмов крана часто используется полиспаст [1].

Полиспастом называют систему подвижных и неподвижных блоков, огибаемых гибким элементом (канатом или цепью), используемую для выигрыша в силе (силовые полиспасты) или скорости (скоростные полиспасты).

Подвижный блок — это блок, ось которого перемещается в пространстве.

Неподвижный блок — это блок, ось которого неподвижна.

Рассмотрим силы, действующиена неподвижный блок (рис.1, а).

Скорость каната при огибании неподвижного блока не изме­няется. При движении каната неподвижный блок приводится во вра­щение силами трения, возникающими между канатом и ручьем (ка­навкой) блока. При этом натяжение S₂ сбегающей ветви каната будет больше натяжения S₁ набегающей ветви на сопротивление жесткости каната и сопротивление трения в подшипниках блока (рис. 1):

S₂=S₁+W_Ж+W_ОП,

где W_Ж — сопротивление жесткости каната, приведенное к ободу блока; W_ОП — сопротивление в подшипниках блока, приведенное к ободу блока.

В этой формуле не учтено дополнительное сопротивление трения каната о реборду блока в момент набегания и сбегания каната, воз­никающее при отклонении каната от плоскости блока.

Вследствие жесткости канат при набегании на блок не сразу входит в его ручей, а при сбегании не сразу приобретает прямолиней­ное положение. Натяжение S₁ (рис. 1, б) приложено на плече (D/2 + b), а усилие (S₁ + W_Ж) на плече (D/2 — b).

Из суммы моментов сил, действующих на блок, имеем

,

,

где j — коэффициент жесткости, определяемый экспериментально и показываю­щий, какую часть рабочего натяжения составляет сопротивление жесткости каната. Для определения сопротивления трения в опоре блока рассмо­трим общий случай, когда набегающая и сбегающая ветви каната не параллельны. При определении равнодействующей S сил натя­жения S₁ и S₂ для расчета сопротивления трения в опоре блока можно с достаточной точностью принять S₁ = S₂ (рис. 1, а), так как сопротивление жесткости каната по сравнению с рабочим натя­жением незначительно.

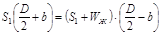Тогда

,

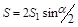где a — угол обхвата блока канатом.

Момент, создаваемый силами трения в опоре диаметром d,

,

где f — коэффициент трения в подшипниках блока (обычно f =0,1..0,15).

Сопротивление в подшипниках блока, приложенное к его ободу,

.

Следовательно,

.

Если на ветвь каната натяжением S₁ будет действовать сила тяжести груза G, то коэффициент полезного действия неподвиж­ного блока будет представлять собой отношение полезной работы Gh = S₁h к затраченной работе S₂h (здесь h — высота подъема груза):

.

Из анализа этой формулы видно, что с увеличением угла об­хвата a и жесткости каната уменьшается коэффициент полезного действия блока.

При a= 180°

.

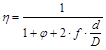Таким образом, при подъеме, огибающим непо­движный направляющий блок, рабочее натяжение сбегающей ветви (см. рис. 1, а)

,

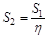При опускании груза рабочее натяжение набегающей ветви

.

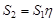Следовательно, наличие сопротив­лений на блоке при опускании груза приводит к уменьшению внешнего рабочего натяжения. В расчетах значения КПД блоков обычно принимают независимо от жесткости канатов и угла обхвата.

Рассмотрим систему с подвижным блоком для выигрыша в силе, имеющую блок 3, ось которого перемещается в про­странстве (рис. 2, а). Один конец каната неподвижно закреплен на конструкции, другой конец — на барабане 4. Сила тяжести поднимаемого груза прило­жена к оси блока. При подъеме груза в набегающей ветви создается натяжение S₁, а в сбегающей S₂ = S_mах. В идеальном случае (без учета сопротивлений) S₁ = S₂ = G/2. При учете сопротивлений при подъеме груза весом G ветвь каната, набегающая на барабан, должна иметь натяжение S₂ > G/2. При подъеме груза на высоту h на барабан наматывается канат длиной 2h. Обозначив скорость подъема груза через V_ГР, скорость ветви каната, набегающей на ба­рабан через V_К из соотношения V_ГР/Vк = h/2h находим V_K = 2V_ГР, т. е. скорость ветви каната, набегающей на барабан, в 2 раза больше скорости подъема груза. Скорость каната в ветви 1 равна нулю, а в ветви 2 — 2V_ГР. Следовательно, при переходе каната через под­вижный блок скорость каната увеличивается на 2V_ГР.

Максимальное натяжение каната с учетом сопротивлений опре­деляют, исходя из следующих соотношений:

при подъеме груза

; ;

;

.

При опускании груза

; ;

;

откуда

.

Коэффициент полезного действия подвижного блока

.

Подставив в эту формулу значение коэффициента полезного дей­ствия неподвижного блока при a= 180°, получим

Сравнивая коэффициент полезного действия подвижного и не­подвижного блоков

можно сделать вывод о том, что сопротивления в подвижных блоках всегда меньше, чем в неподвижных.

В расчетах значения КПД для подвижных и неподвижных бло­ков принимают одинаковыми: для блоков на подшипниках качения h= 0,97... 0,98, а для блоков на подшипниках скольжения h = 0,94... 0,96.

Рассмотрим систему с подвижным блоком для выигрыша в ско­рости (рис. 2, б). Система имеет следующие основные элементы: барабан 4 с грузовым канатом 5, один конец которого закреплен на барабане, а другой — на оси подвижного блока 6; через подвижный блок пере­кинут канат 7, один конец которого закреплен на неподвижной оси 5, а к другому подвешен груз весом G. При подъеме груза на вы­соту 2h ось подвижного блока 6 поднимается на высоту h. Следова­тельно, скорость подъема груза в 2 раза больше скорости подъема подвижного блока.

Для подвижного блока 6 при подъеме груза натяжение в набе­гающей ветви S₁ = G, а в сбегающей S₂. Коэффициент полезного действия подвижного блока для выигрыша в скорости

.

Учитывая, что

,

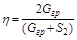получаем

.

Откуда

.

Следовательно, Р = G + G (2 - h)/h = 2G/h. Таким образом, для подъема груза весом G к подвижному блоку следует прило­жить усилие Р, более чем в 2 раза превышающее G.

Наибольшее применение в грузоподъем­ных машинах находят одинарные (рис. 3) и сдвоенные (рис. 4) силовые полиспасты [2]. В схемах, представленных на рис. 3, один конец каната закреплен на барабане, другой — на неподвижной части конструкции крана или в крюковой подвеске, барабан имеет нарезку в одну сторону. Такие полиспасты называют

одинарными.

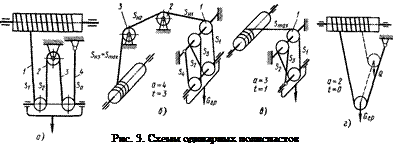На схемах, представленных на рис. 4, оба конца каната закреп­лены на барабане, а барабан имеет нарезку в правую и левую стороны. Такие полиспасты принято называть сдвоенными. Их можно рас­сматривать как два одинарных полиспаста.

Во многих кранах по конструктивным соображениям механизм подъема груза расположен не над крюковой подвеской. В этом слу­чае появляется необходимость в установке между полиспастом и барабаном неподвижных направляющих блоков 1, 2, 3 (рис. 3, б).

Рассмотрим для одинарных полиспастов определение скорости ветви каната, набегающей на барабан (рис. 3, а). Зададимся ско­ростью подъема груза V_ГР. Скорость каната в ветви 4 равна нулю. Скорость каната при переходе через каждый подвижный блок уве­личивается на 2 V_ГР, тогда скорость в ветви 1 будет 4 V_ГР.

Отношение скорости в ветви каната, набегающей на барабан, к скорости подъема груза называют кратностью полиспаста. Ее обо­значили буквой а. На рис. 4 а, б а = 4. Для сдвоенного поли­спаста (рис. 4, а) скорость в ветви 2 равна нулю, в ветви 1 после подвижного блока 2 V_ГР. Для сдвоенных полиспастов также соответ­ствует принятое определение кратности полиспаста, т.е. в схеме на рис. 4, а а = 2.

Для определения максимального натяжения S_max каната при подъеме груза рассмотрим схему на рис. 3, а. Сила тяжести под­нимаемого груза G приложена к крюку. В состоянии покоя натя­жение во всех ветвях каната одинаково

S₁= S₂ =... = S_a = G/a.

При подъеме груза натяжение каждой ветви каната вследствие имеющихся в системе сопротивлений различно и максимальное зна­чение натяжения S₁ = S_max будет в ветви каната, набегающей на барабан, а минимальное в последней ветви Sa.

Натяже­ние в каждой ветви полиспаста

S₁ = S_max; S₂ =S_max×h

…

S_a = S_a-1h = S_max×h^a-1

Тогда

G = S₁ + S₂ + …+ S_a = S_max(l + h + h²… + h^а-1).

В этой формуле выражение в скобках представляет геометрическую прогрессию, определив ее, получим

.

Откуда

.

Коэффициент полезного действия полиспаста

,

где Gh — полезная работа; S_max ah — затраченная работа. Подставляя в эту формулу значения S_max, получим .

Таким образом, максимальное натяжение ветви каната при подъеме груза

S_max = G/ah_П.

При опускании груза распределение натяжений в ветвях поли­спаста изменяется. Минимальное натяжение S₁=Smin возникнет в ветви каната, сбегающей с барабана, а максимальное — в послед­ней ветви S_a=S_max= G/(ah_П). Это значение используют при расчете узла крепления конца каната.

В схеме 3, б между барабаном и полиспастом расположены на­правляющие блоки 1, 2, 3. Натяжение S₁ определяют аналогично рассмотренной выше схеме. Натяжение в набегающей ветви каната на барабан S_Н3 = Smax будет больше натяжения S₁ на значение сопротивлений в направляющих блоках, что в общем виде можно записать

S_max = S₁/h^t,

где t — число направляющих блоков.

Учитывая эту формулу, имеем

.

Недостатком схем одинарных полиспастов является нежелательное изменение нагрузки, действующей на опоры барабана при подъеме или опускании груза.

В схеме полиспаста, представленной на рис. 3, г, груз при опускании и подъеме перемещается не по вертикали, а по наклонной траектории (показано штриховой линией). В одинарных полиспастах с нечетной кратностью полиспаста (рис. 3, б) имеется большее стремление к кручению крюковой подвески, чем в полиспастах с четной кратностью.

Сдвоенные полиспасты имеют широкое применение в механизмах подъема многих кранов — мостовых, консольных, козловых и дру­гих, где постоянство давлений на опоры барабана во время подъема или спуска груза важно для обеспечения равномерной загрузки металлоконструкции моста под обоими рельсами.

Сдвоенный полиспаст, показанный на рисунке 4, а имеет верхний блок 3, назы­ваемый уравнительным. Он предназначен для выравнивания длины ветвей каната при неравномерном их вытягивании. Уравнительный блок может быть заменен рычагом (рис. 4, б). При этом вместо одного каната устанавливают два, что особенно выгодно в механиз­мах с большой кратностью полиспаста, для которых требуются ка­наты большой длины. При четной кратности (рис. 4, а) уравнительный блок 3 расположен на неподвижной оси, при нечетной крат­ности — на подвижной оси крюковой подвески (рис. 4, б).

Натяжение S_max для сдвоенного полиспаста определяют анало­гично расчету одинарного полиспаста, причем считают, что на каж­дый полиспаст действует G/2:

.

Рассмотрим схемы сдвоенных полиспастов на примере расчета ме­ханизма подъема груза, мостового крана общего назначения грузоподъемностью Q = 12,5 т, высотой подъема груза Н = 12 м, скоростью подъема груза V_ГР= 8 м/мин, режима работы - тяжелый; принята схема сдвоенного полиспаста с различной кратностью, а = 2, 3 и 5. При расчете получены следующие данные:

Кратность................. 2 3 5

Расчетные данные:

максимальное усилие каната S_max, Н... 30 966 20 854 12 760

диаметр каната d, mm.......... 18 15 12

диаметр барабана Dб, mm......... 450 375 300

частота вращения барабана n, об/мин... 11,32 20,38 42,46

частота вращения э/двигателя, об/мин 950 950 950

передаточное число редуктора и...... 83,92 46,61 22,30

длина барабана L, мм .......... 1 060 1 392 2 159

Из расчетных данных видно, что с уменьшением кратности полиспаста уве­личивается передаточное число редуктора, а с увеличением кратности возрастает длина барабана. В рассмотренном примере целесообразно отказаться от примене­ния полиспаста с а = 2, так как при этой кратности получено высокое значение передаточного отношения, которое не соответствует нормативным данным. Схема полиспаста с а= 5, также не пригодна вследствие получения большой длины барабана.

Дата добавления: 2015-08-10